Carnet de bac
Annales
Vol Zéro-G |
SUP ➔ |
| Liban 2016 - Exercice 1 - 6 points |
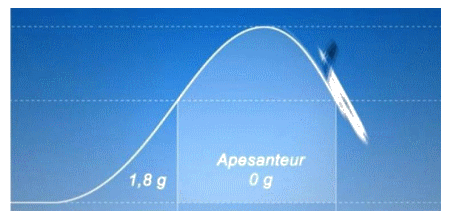
Au printemps 2015, l’airbus A310 Zéro-G a réalisé ses premiers vols scientifiques. Exploité par une filiale du Centre National d’Études Spatiales (CNES), cet avion permet de simuler des conditions d’apesanteur en décrivant des trajectoires paraboliques. Les scientifiques peuvent ainsi mener des expériences sans avoir recours aux missions spatiales. | ||||||||||||
|
Document 1 - Trajectoire parabolique de l’A310 Zéro-G
Pour que les passagers et le matériel embarqués dans l'Airbus A310 Zéro-G soient en apesanteur dans le référentiel de l'avion, et qu'ils se mettent à y "flotter", il faut que l'avion soit en chute libre. Dans le référentiel terrestre, un corps est en chute libre lorsque la seule force qui s'exerce sur lui est le poids. Comment mettre l'avion en condition de "chute libre", peut-on se demander. Rien de plus "simple". Il suffit que le pilote de l'avion arrive à suivre la bonne trajectoire parabolique. Extrait d’un article de presse | ||||||||||||
Document 2 - Caractéristiques du vol parabolique
| ||||||||||||
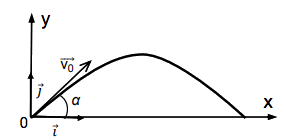
Données :
On se place dans le référentiel terrestre considéré comme galiléen sur la durée d’une parabole.
On étudie le mouvement dans le repère xOy donné ci-contre, le point O étant le début de la parabole. On considère que l’intensité de la pesanteur terrestre est constante lors d’un vol Zéro-G et qu’elle est égale à g = 9,8 N·kg-1.
|
||||||||||||