Carnet de cours
Ondes et rayonnements
11. Ondes |
||||
| Onde, onde progressive et onde stationnaire | ||||
| • On appelle onde la propagation d'une perturbation associée à un transport d'énergie sans transport de matière. | ||||
| • On dit qu'une onde est progressive si elle se propage ; elle est dite stationnaire si elle semble ne pas se propager à cause de la présence de nœuds et de ventres. | ||||
Onde transversale et onde longitudinale |
||||
| • On dit qu'une onde est transversale si sa direction de propagation est orthogonale à sa direction de perturbation ; elle est dite longitudinale si sa direction de propagation est identique à sa direction de perturbation. | ||||
Onde mécanique |
||||
| • On dit qu'une onde est mécanique si elle nécessite un milieu matériel (constitué de particules présentant une masse non-nulle) pour se propager. | ||||
| Ondes électromagnétiques et ondes de matière | ||||
| Les ondes électromagnétiques ainsi que les ondes de matière ne nécessitent pas de milieu matériel pour propager, elle ne sont donc pas des ondes mécaniques. | ||||
Onde périodique |
||||
| • La période d'une onde, notée T et mesurée en secondes (s), est la durée au bout de laquelle l'onde se répète indentique à elle-même. | \(\displaystyle \mathrm{ Ψ (t) = Ψ (t+T) }\) | |||
| • La fréquence d'une onde, notée f et mesurée en hertzs (Hz), s'écrit | \(\displaystyle \mathrm{ f= \frac{1}{T} }\) | |||
| • La pulsation, notée \(\displaystyle \mathrm{ ω }\) et mesurée en rad·s-1, d'un phénomène périodique de période T s'écrit | \(\displaystyle \mathrm{ ω = \frac{2 \ π}{T} }\) | |||
| Pulsation et fréquence | ||||
| D'après les définitions de la fréquence et de la pulsation | \(\displaystyle \mathrm{ ω = 2 \ π \ f }\) | |||
| • La longueur d'onde d'une onde, notée \(\displaystyle \mathrm{ λ }\) et mesurée en mètres, est la distance au bout de laquelle l'onde se répète indentique à elle-même. | \(\displaystyle \mathrm{ λ }\) | |||
| Double périodicité | ||||
| D'après la définition de la vitesse, si un phénomène périodique dans le temps se propage, alors on peut lui associer une période spatiale appelée longueur d'onde tel que | \(\displaystyle \mathrm{ λ =v \ T }\) | |||
| ou encore | \(\displaystyle \mathrm{ λ =\frac{v}{f} }\) | |||
Effet Doppler |
➔ | |||
| Si l'émetteur d'une source périodique émettant un signal de fréquence fe se déplace par rapport à un récepteur, alors celui-ci perçoit ce signal avec une fréquence fp telle que | \(\displaystyle \mathrm{ f_p =\frac{v_{onde}-v_{récep}}{v_{onde}-v_{émet}} \ f_e }\) | |||
Dispersion et diffraction |
||||
| • On dit qu'il y a dispersion d'une onde périodique lorsque sa célérité dans un milieu, dépend de sa fréquence. | \(\displaystyle \mathrm{ v = v (f) }\) | |||
| • On dit qu'il y a diffraction d'une onde périodique lorsqu'il y a ouverture d'un faisceau de l'onde au passage d'un obstacle ou d'une ouverture. | ||||
Interférences constructives ou destructives |
||||
| • On dit qu'il y a interférence lorsque plusieurs ondes se superposent en une région de l'espace. | ||||
| • Une interférence est dite constructive si l'amplitude de l'onde résultant de la superposition est supérieure aux amplitudes des ondes superposées. Elle est dite destructive dans le cas contraire. | ||||
Onde de matière |
||||
| • Une onde de matière est une onde associée à un corps matériel, c'est-à-dire associée à un corps de masse non-nulle. | ||||
| Loi de de Broglie | ||||
| A toute particule matérielle animée d'une quantité de mouvement p, est associée une onde de matière dont la longueur d'onde s'écrit | \(\displaystyle \mathrm{ λ = \frac{h}{p} }\) | |||
|
||||
| Quantité de mouvement associée à un photon | ||||
| D'après les loi de Planck et de de Broglie on peut associer à un photon véhiculant un quantum d'énergie \(\displaystyle \mathrm{ ε }\), une quantité de mouvement | \(\displaystyle \mathrm{ p = \frac{ε}{c} }\) | |||
12. Optique géométrique |
|||||||||||||||||||||||
| Rayon lumineux et indice de réfraction | |||||||||||||||||||||||
| • On appelle rayon lumineux la direction de propagation de la lumière entre deux points distincts. | |||||||||||||||||||||||
| • On dit qu'un milieu est transparent s'il laisse passer la lumière et il est dit opaque dans le cas contraire. | |||||||||||||||||||||||
| • L'indice de réfraction, noté n et mesuré sans unité, d'un milieu transparent à travers lequel la lumière se propage à la vitesse v s'écrit | \(\displaystyle\mathrm{n = \frac{c}{v}}\) | ||||||||||||||||||||||
| • On dit qu'un milieu est homogène si son indicde de réfraction est le même en tout point | |||||||||||||||||||||||
|
|||||||||||||||||||||||
| Propagation rectiligne de la lumière | |||||||||||||||||||||||
| D'après les lois de l'électromagnétisme on montre que le chemin emprunté par la lumière dans un milieu homogène est rectiligne. | |||||||||||||||||||||||
Diamètre apparent |
|||||||||||||||||||||||
| • Le diamètre apparent, noté \(\displaystyle\mathrm{α}\) et mesuré en radians (rad), d'un objet de dimension d aperçu depuis une distance D, grande devant d, vaut | \(\displaystyle\mathrm{α = \frac{d}{D}}\) | ||||||||||||||||||||||
| • Le pouvoir séparateur de l'oeil, noté \(\displaystyle\mathrm{θ}\) et mesuré en radians (rad), est le plus petit diamètre apparent sous lequel l'oeil est capable d'apercevoir deux points distincs | |||||||||||||||||||||||
|
|||||||||||||||||||||||
Changement de milieu et dioptre |
|||||||||||||||||||||||
| • On appelle dioptre la surface de séparation entre deux milieux d'indices de réfraction différents. | |||||||||||||||||||||||
| Loi de Descartes | |||||||||||||||||||||||
| D'après les lois de l'électromagnétisme on montre qu'au passage d'un dioptre, la direction de propagation de la lumière est modifiée tel que | \(\displaystyle\mathrm{n \ sin \ i = n' \ sin \ r'}\) | ||||||||||||||||||||||
|
● i est l'angle entre la direction du rayon incident et la direction normale au dioptre ;
● r est l'angle entre la direction du rayon réfracté et la direction normale au dioptre ; ● n est l'indice du milieu d'où provient le rayon incident ; ● n' est l'indice du milieu où émerge le rayon réfracté. | 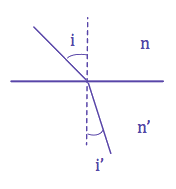 |
||||||||||||||||||||||
Incidence maximale |
|||||||||||||||||||||||
| D'après la relation de Descartes, si le rayon passe d'un milieu moins réfringent d'indice de réfraction n vers un milieu plus réfringent d'indice de réfraction n' alors | \(\displaystyle\mathrm{n < n'}\) | ||||||||||||||||||||||
| donc il existe un angle d'incidence limite iℓ tel que | \(\displaystyle\mathrm{sin \ i_{ℓ} = \frac{n}{n'}}\) | ||||||||||||||||||||||
| donc, si i>iℓ alors il n'y a pas de réfraction possible, le rayon est totalement réfléchi. | |||||||||||||||||||||||
Milieu dispersif et phénomène de dispersion |
|||||||||||||||||||||||
| • Un milieu est dit dispersif si la vitesse de propagation de la lumière à travers ce milieu dépend de sa fréquence de radiation. | |||||||||||||||||||||||
| Loi de Cauchy | |||||||||||||||||||||||
| Il existe une série de coefficients ai tel que | \(\displaystyle\mathrm{n = a_0 + \frac{a_1}{λ^2} + \frac{a_2}{λ^4}+...}\) | ||||||||||||||||||||||
|
|||||||||||||||||||||||
|
|||||||||||||||||||||||
13. Lentilles minces |
||
| Lentille mince, axe et centre optique | ||
| • On appelle lentille mince un corps transparent délimité par deux portions de dioptres sphériques dont les rayons sont grands devant l'épaisseur au centre de la lentille. | ||
| • On appelle convergente une lentille dont l'épaisseur au centre est plus grande que l'épaisseur aux extrémités. Par convention, une lentille convergente est représentée de la manière ci-contre |  |
|
| • On appelle axe optique d'une lentille mince, l'axe de symétrie de la lentille. | ||
| • On appelle centre optique d'une lentille mince, le point d'intersection entre son plan de symétrie et l'axe optique. | ||
| • On dit qu'un système est stigmatique si l'image qu'il donne d'un point est un point. | ||
| Stigmatisme d'une lentille mince | ||
| On montre qu'une lentille mince est un système stigmatique. | ||
Foyers objet et image |
||
| • On appelle foyer objet, noté F, le point dont l'image est située à l'infini sur l'axe optique. | \(\displaystyle\mathrm{F \longrightarrow \infty}\) | |
| • On appelle foyer image, noté F', le point dont l'antécédent un point situé à l'infini sur l'axe optique. | \(\displaystyle\mathrm{\infty \longrightarrow F'}\) | |
| Symétrie des foyers | ||
| Dans le cas d'une lentille mince, on montre que les foyers objet et image sont symétriques par rapport au centre optique de la lentille. | \(\displaystyle\mathrm{ OF = OF' }\) | |
Distance focale et vergence |
||
| • La distance focale, notée f et mesurée en m, d'une lentille mince, est la distance qui sépare le centre optique O de la lentille et le foyer image F'. | \(\displaystyle\mathrm{f = OF'}\) | |
| • La vergence, notée v et mesurée en dioptrie ( δ ) ou m·-1, d'une lentille mince s'écrit | \(\displaystyle\mathrm{v =\frac{1}{f}}\) | |
| Loi de conjugaison de Descartes | ||
| D'après la loi de la réfraction de Descartes, on montre que dans les conditions de Gauss et pour une lentille mince de distance focale f, la position d'un point A' image d'un point A appartenant à l'axe est donnée par | \(\displaystyle\mathrm{\frac{1}{\overline{OA'}}-\frac{1}{\overline{OA}}=\frac{1}{f}}\) | |
| \(\displaystyle\mathrm{\overline{MN}}\) est la valeur algébrique de la longueur du segment MN, comptée postitivement de gauche à droite le long de l'axe optique et négativement en sens inverse. | ||
| Conditions de Gauss : ➀ Les rayons sont faiblement inclinés par rapport à l'axe optique. ➁ Les rayons sont proches de l'axe optique. |
||
Relation de Newton |
➔ | |
| D'après la relation de conjugaison de Descartes on montre que | \(\displaystyle\mathrm{\overline{FA} \times \overline{F'A'}=-f^2}\) | |
|
Construction géométrique |
||
|
D'après ce qui précède on montre que :
➀ tout rayon passant par le centre optique ne subit aucune déviation ➁ tout rayon passant par le foyer objet émerge parallèlement à l'axe optique ➂ tout rayon parallèle à l'axe optique émerge en passant par le foyer image |
||
Objets et images, réels et virtuels |
||
| • On appelle espace objet le demi-espace contenant le foyer objet. | ||
| • On appelle espace image le demi-espace contenant le foyer image. | ||
| • Un objet est dit réel pour une lentille s'il appartient à l'espace objet de cette lentille, et virtuel s'il appartient à l'espace image. | ||
| • Une image est dite réelle pour une lentille si elle appartient à l'espace image de cette lentille, et virtuelle si elle appartient à l'espace objet. | ||
Grandissement et grossissement |
||
| • Le grandissement, noté \(\displaystyle\mathrm{γ }\) et mesuré sans unité, d'un objet de hauteur AB dont l'image donnée par une lentille a une hauteur A'B' , s'écrit | \(\displaystyle\mathrm{γ = \frac{\overline{A'B'}}{\overline{AB}}}\) | |
| • Le grossissement, noté G et mesuré sans unité, d'un instrument optique est le rapport entre le diamètre apparent \(\displaystyle\mathrm{α}\) d'un objet perçu sans l'instrument optique et le diamètre apparent \(\displaystyle\mathrm{α'}\) du même objet perçu à travers l'instrument | \(\displaystyle\mathrm{G = \frac{α'}{α}}\) | |
| Grandissement d'une lentille | ||
| D'après la relation de conjugaison, on montre que | \(\displaystyle\mathrm{γ = \frac{\overline{OA'}}{\overline{OA}}}\) | |
| Grossissement d'une lunette | ||
| D'après la définition d'une lunette astronomique dont les distances focales de l'objectif et de l'oculaire sont respectivement fobj et foc , on montre que | \(\displaystyle\mathrm{G = \frac{f_{obj}}{f_{oc}}}\) | |
14. Optique ondulatoire |
||
| Onde électromagnétique | ||
| • Une onde électromagnétique est une onde associée à la propagation d'un champ électrique combiné à un champ magnétique. | ||
| • Une pulsation, notée \(\displaystyle\mathrm{ ω }\) et mesurée en rad·s-1, associée à une période T s'écrit : | \(\displaystyle\mathrm{ ω = \frac{2 \ π}{T} }\) | |
Diffraction d'ondes lumineuses |
||
| • On dit qu'il y a diffraction d'une onde périodique lorsqu'il y a ouverture d'un faisceau d'ondes au passage d'un obstacle ou d'une ouverture. | ||
| Diffraction par une ouverture rectiligne | ||
| Si une onde électromagnétique de longueur d'onde λ rencontre un obstacle rectiligne ou une ouverture rectiligne (fente d'Young) de dimension a alors on montre que la demi-ouverture du faisceau lumineux vaut | \(\displaystyle\mathrm{θ \simeq \ \frac{λ}{a}}\) | |
| Diffraction par une ouverture circulaire | ||
| Si une onde électromagnétique de longueur d'onde λ rencontre un obstacle circulaire ou une ouverture circulaire de dimension a alors on montre que la demi-ouverture du faisceau lumineux vaut | \(\displaystyle\mathrm{θ \simeq 1,22 \ \frac{λ}{a}}\) | |
| Figures de diffraction | ||
| Si l'ouverture de diffraction est rectangulaire alors la figure de diffraction est constituée d'une tache rectiligne orientée perpendiculairement à l'orientation de longueur de la source, et de taches latérales situées dans le prolongement de la tache centrale.
Si l'ouverture de diffracton est circulaire alors la figure de diffraction est constituée d'une tache centrale circulaire dite tache d'«Airy» et de cercles concentriques. |
||
| Si λ et a sont du même ordre de grandeur alors le phénomène est perceptible. | ||
Interférence d'ondes lumineuses |
||
| • La différence de chemin optique, notée δ et mesurée en mètres, est la différence de longueur entre les distances parcorures par deux ondes issues de deux points sources respectifs S1 et S2 et allant jusqu'à un point M. | \(\displaystyle\mathrm{ δ = S_2M - S_1M }\) | |
| • Deux ondes sont dites en phase si elles ont le même terme de phase au cours du temps en un point M. | ||
| • Deux ondes sont dites en opposition de phase si leurs termes de phase sont décalés de \(\displaystyle\mathrm{ \frac{π}{2} }\) au cours du temps en un point M. | ||
| • On dit que l'interférence est constructive si les ondes qui se superposent sont en phase ; destructive si elles sont en opposition de phase. | ||
| • On appelle frange d'interférence une partie sombre ou brillante de l'espace correspondant à des interférences respectivement déstructives et constructives. | ||
| • L'interfrange, notée i et mesurée en mètre, est la distance qui sépare deux franges brillantes consécutives. | ||
| Interfrange d'interférence, fentes d'Young | ➔ | |
| Si on considère des figures d'interférences sur un écran situé à une distance D de deux sources ponctuelles monochromatiques de longueur d'onde (dans le vide) \(\displaystyle \mathrm{ λ }\), et séparées d'un écart b alors on montre que la valeur de l'interfrange vaut | \(\displaystyle\mathrm{i \simeq \ \frac{λ }{b} \ D}\) | |
Localisation des franges d'interférence |
||
| Au point situé sur l'écran d'obsevation au niveau de l'axe de symétrie des deux sources, les ondes sont en phase et la frange d'interférence est brillante. | ||
| Si en un point M de l'écran d'observation \(\displaystyle\mathrm{ δ = k \ λ \ (k \in \mathbb{N}) }\), alors les ondes sont en phase donc l'interférence est construtive et la frange est brillante. | \(\displaystyle\mathrm{ δ =k \ λ }\) | |
| Si en un point M de l'écran d'observation \(\displaystyle\mathrm{ δ = (k+\frac{1}{2}) \ λ \ (k \in \mathbb{N}) }\), alors les ondes sont en opposition de phase donc l'interférence est destructive et la frange est sombre. | \(\displaystyle\mathrm{ δ = \left( k + \frac{1}{2} \right) \ λ}\) | |
Relation de Bragg |
||
| Si on éclaire un plan critallin avec un rayonnement de longueur d'onde \(\displaystyle\mathrm{ λ }\) et une incidence \(\displaystyle \mathrm{ θ }\) par rapport à la direction normale au plan, et si la distance interréticulaire (séparant les plans cristallins deux à deux) vaut d, alors les maxima d'intensité sont observés dans les cas suivants où n est un entier : | \(\displaystyle\mathrm{ n \ λ = 2 \ d \ sinθ }\) | |
Emission stimulée et laser |
||
| • L'appellation LASER signifie light amplification by stimulation and emission of radiation, soit "Amplification de lumière par stimulation et émission de radiation". | ||
| • On dit qu'il y a émission stimulée si l'émission d'un photon est due à l'action d'un photon incident de même énergie qui n'est pas absorbé lors du processus. | ||
| Propriétés d'un Laser | ||
| D'après son principe de fonctionnement, un rayon laser est monochromatique, monodirectionnel et très énergétique. | ||
15. Rayonnements |
||||||||||||||||||||||||||||||||||||||
| Spectres et synthèse des couleurs | ||||||||||||||||||||||||||||||||||||||
| • On appelle spectre, la représentation donnant l'intensité ou la couleur d'une radiation en fonction de sa fréquence ou de sa longueur d'onde dans le vide. | ||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||
| • Un spectre est dit continu s'il est dû à la superposition de toutes les radiations existantes. | ||||||||||||||||||||||||||||||||||||||
| • Un spectre est dit d'émission s'il est dû à la superposition de radiations émises par une ou plusieurs substances ; il est dit d'absorption s'il est dû à l'élimination de radiations d'un spectre continu. | ||||||||||||||||||||||||||||||||||||||
| • Un spectre est dit de raie s'il a l'aspect de fines raies claires ou sombres ; il est dit de bande s'il a l'aspect de larges bandes claires ou sombres. | ||||||||||||||||||||||||||||||||||||||
| • La synthèse d'une couleur est dite additive si elle est réalisée par superposition de radiations ; elle est dite soustractive si elle est réalisée par élimination de radiations à partir d'un continuum de radiations. | ||||||||||||||||||||||||||||||||||||||
Rayonnement par transition énergétique |
||||||||||||||||||||||||||||||||||||||
| • On appelle niveau d'énergie atomique ou moléculaire, caractérisé par un nombre quantique n, un état d'énergie d'un électron lié à un atome ou à une molécule. | \(\displaystyle \mathrm{E_n}\) | |||||||||||||||||||||||||||||||||||||
| • Un quantum d'action d'énergie, noté \(\displaystyle \mathrm{ε }\) et mesuré en joules, est la quantité d'énergie véhiculée lors d'une transition électronique d'un niveau d'énergie Ei vers un niveau Ef. | \(\displaystyle \mathrm{ε = | \ E_f - E_i \ |}\) | |||||||||||||||||||||||||||||||||||||
| • On appelle photon l'entité élémentaire et individuelle véhiculant un quatum d'énergie \(\displaystyle \mathrm{ε }\) . | ||||||||||||||||||||||||||||||||||||||
| • Un ion monoatomique est appelé hydrogénoïde s'il ne possède qu'un seul électron. | ||||||||||||||||||||||||||||||||||||||
| Cas de l'atome d'hydrogène | ➔ | |||||||||||||||||||||||||||||||||||||
| D'après les lois de la mécanique quantique on montre que le niveau d'énergie En (en eV) du niveau n d'un atome d'hydrogène s'écrit | \(\displaystyle\mathrm{E_n = - \frac{E_0}{n^2}}\) | |||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||
| Pour un ion hydrogénoïde de numéro atomique Z, on montre que | \(\displaystyle\mathrm{E_n = - E_0 \ \frac{Z^2}{n^2}}\) | |||||||||||||||||||||||||||||||||||||
|
Niveaux d'énergie moléculaires |
||||||||||||||||||||||||||||||||||||||
| D'après les lois de la mécanique quantique on montre qu'il existe des niveaux d'énergie de rotation et d'oscillation affectés aux molécules. | ||||||||||||||||||||||||||||||||||||||
|
Loi de Planck |
||||||||||||||||||||||||||||||||||||||
| D'après les lois de la mécanique quantique, l'énergie \(\displaystyle\mathrm{ε }\) véhiculée par un quantum associé à un rayonnement de fréquence \(\displaystyle\mathrm{ν}\) s'écrit | \(\displaystyle\mathrm{ε = h \ ν}\) | |||||||||||||||||||||||||||||||||||||
|
Spectres d'émission et d'absorption |
||||||||||||||||||||||||||||||||||||||
| D'après la loi de Planck : | ||||||||||||||||||||||||||||||||||||||
| - si un électron subit une transition d'un niveau d'énergie supérieur vers un niveau inférieur, alors il y a émission d'un photon et réciproquement ; le spectre correspondant présente des raies claires sur un fond sombre : un spectre d'émission | ||||||||||||||||||||||||||||||||||||||
| - si un électron subit une transition d'un niveau d'énergie inférieur vers un niveau supérieur, alors il y a absorption d'un photon et réciproquement ; le spectre correspondant est continu présentant des raies sombres : un spectre d'absorption. | ||||||||||||||||||||||||||||||||||||||
|
Loi de combinaison de Ritz |
||||||||||||||||||||||||||||||||||||||
| D'après la loi de Planck, lors d'une transition d'un niveau n vers un niveau inférieur p (p < n), le rayonnement émis a une longueur d'onde tel que | \(\displaystyle\mathrm{\frac{1}{λ} = R_H \ \left( \frac{1}{p^2} - \frac{1}{n^2} \right) }\) | |||||||||||||||||||||||||||||||||||||
| où RH est appellée constante de Rydberg et s'écrit | \(\displaystyle\mathrm{ R_H =\frac{E_0}{h \ c} }\) | |||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||
• On appelle luminescence l'émission spontanée de photons d'un corps dans le domaine visible après avoir été éclairé. On parle de fluoresence si elle se fait rapidement, et de phosphorescence si elle se fait lentement. |
||||||||||||||||||||||||||||||||||||||
Rayonnement par agitation thermique |
||||||||||||||||||||||||||||||||||||||
| • On appelle corps noir tout matériau susceptible d'absorber toutes les radiations. | ||||||||||||||||||||||||||||||||||||||
| • On appelle source chaude un corps dont la température est suffisamment élevée (plusieurs milliers de kelvins) pour émettre des radiations dnas le domaine visible. | ||||||||||||||||||||||||||||||||||||||
| Loi du déplacement de Wien | ||||||||||||||||||||||||||||||||||||||
| D'après la loi de Planck donnant l'énergie rayonnée par un corps noir constituant une source chaude, on montre qu'un corps noir porté à une température T, émet un rayonnement dont l'intensité maximale est obtenue pour le rayonnement de longueur d'onde λmax | \(\displaystyle\mathrm{λ_{max} = \frac{K}{T}}\) | |||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||
16. Signaux |
||||||||||||||||||||||||||||||
| Son pur et son complexe | ||||||||||||||||||||||||||||||
| • On dit qu'un son est pur s'il est constitué d'une seule fréquence. | ||||||||||||||||||||||||||||||
| • On dit qu'un son est complexe s'il est constitué de plusieurs fréquences. | ||||||||||||||||||||||||||||||
| • On appelle hauteur d'un son la fréquence du fondamental de ce son. | ||||||||||||||||||||||||||||||
| • On appelle timbre sonore, l'ensemble des harmoniques qui le composent. | ||||||||||||||||||||||||||||||
| Puissance et niveau sonore | ||||||||||||||||||||||||||||||
| • L'intensité sonore, notée I et mesurée en W·m-2, d'un signal sonore véhiculant une puissance Ps répartie sur une aire S s'écrit | \(\displaystyle\mathrm{I = \frac{P_s}{S}}\) | |||||||||||||||||||||||||||||
| • Le niveau sonore, noté L (comme level) et mesuré en décibels (dB), d'une onde sonore d'intensité I s'écrit
où I0=10-12 W·m-2 est le seuil d'audibilité de l'oreille humaine |
\(\displaystyle \mathrm{L = 10 \ log \frac{I}{I_0}}\) | |||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||
| Niveau sonore en fonction de la distance | ||||||||||||||||||||||||||||||
| D'après l'expression du niveau sonore, si une onde présente un niveau I à une distance R et un niveau I' à une distance R' alors | \(\displaystyle \mathrm{I' = I + 20 \ log \frac{R}{R'}}\) | |||||||||||||||||||||||||||||
Signal sismique : échelle de Richter |
||||||||||||||||||||||||||||||
| • La magnitude d'un séisme, notée M et mesurée sans unité, est exprimée par le déplacement maximum ℓmax que subit le stylet du sismographe au moment du séisme, en comparaison avec le déplacement moyen ℓ0 du stylet en absence de séisme | \(\displaystyle \mathrm{M = log \frac{ℓ_{max}}{ℓ_0}}\) | |||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||
Conversion analogique-numérique (CAN) |
||||||||||||||||||||||||||||||
| • Un signal est dit analogique lorsque sa valeur varie de manière continue, il est dit numérique lorsque sa valeur varie de manière discontinue. | ||||||||||||||||||||||||||||||
| • On appelle conversion analogique-numérique le processus au cours duquel un signal analogique est transformé en signal numérique selon trois étapes successives d'échantillonnage, de quantification et de numérisation ou encodage. | ||||||||||||||||||||||||||||||
| • On appelle échantillonnage l'étape consistant à mesurer la valeur du signal analogique à intervalles de temps réguliers appelée période d'échantillonnage Te. | ||||||||||||||||||||||||||||||
| • On appelle fréquence d'échantillonnage notée fe et mesurée en Hz, associée à la période d'échantillonnage Te | \(\displaystyle \mathrm{f_e =\frac{1}{T_e} }\) | |||||||||||||||||||||||||||||
| • On appelle quantification l'étape consistant à affecter une valeur discrète à chaque échantillon en fonction de la résolution (ou pas). | ||||||||||||||||||||||||||||||
| • On appelle pas ou résolution noté p et mesuré dans l'unité du signal analogique numérisé dont la valeur est comprise entre Umax et Umin et quantifié selon n bits | \(\displaystyle \mathrm{p =\frac{U_{max} - U_{min}}{2^n-1} }\) | |||||||||||||||||||||||||||||
| • On appelle numérisation ou encodage l'étape consistant à attribuer un nombre binaire à la valeur quantifiée. | ||||||||||||||||||||||||||||||
| • Un bit est l'unité d'un chiffre en système binaire. | ||||||||||||||||||||||||||||||
| • Un byte est la plus petite unité adressable d'un ordinateur. | ||||||||||||||||||||||||||||||
| • Un octet est un byte de huits bits. | ||||||||||||||||||||||||||||||
| • Les multiples binaires sont les suivants : | ||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||
• On appelle débit, noté D et mesuré en Mo·s-1, la quantité d'octet transférée par seconde. |
\(\displaystyle \mathrm{ D= \frac{N}{Δt} }\) |
|||||||||||||||||||||||||||||
• On appelle latence, notée L et mesuré en secondes, la durée minimale de communication d'un signal prenant en compte la durée de transmission \(\displaystyle \mathrm{ Δt_{tr} }\) et la durée de propagation \(\displaystyle \mathrm{ Δt_{pr} }\) . |
\(\displaystyle \mathrm{ L= Δt_{tr} + Δt_{pr} }\) |
|||||||||||||||||||||||||||||
| • Le pixel (pour "picture element"), noté px, est l'unité de base d'une image numérique, composée de trois sous-pixels : un rouge, un vert et un bleu (RVB ou RGB en anglais). | ||||||||||||||||||||||||||||||
| Premières conversions décimale - binaire | ||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||
| Restitution artificielle des couleurs | ||||||||||||||||||||||||||||||
| Les sous-pixels étant des sources premières de lumières, l'image formée par un écran est obtenue par synthèse additive. | ||||||||||||||||||||||||||||||
|
Théorème de Shannon |
||||||||||||||||||||||||||||||
| Pour effectuer une numérisation de bonne qualité, la fréquence d'échantillonnage fe doit être supérieure au double de la fréquence la plus élevée fmax du signal à convertir. | \(\displaystyle \mathrm{ f_e > 2 \ f_{max} }\) | |||||||||||||||||||||||||||||
• On appelle atténuation, notée A et mesurée en décibels (dB), entre la puissance d'entrée Pe d'un signal et la puissance de sortie Ps de ce même signal aux extrémités d'un câble ou d'une fibre optique la quantité |
\(\displaystyle \mathrm{ A=10 \ log \frac{P_e}{P_s} }\) |
|||||||||||||||||||||||||||||
| Loi sur l'atténuation | ||||||||||||||||||||||||||||||
| Il existe un coefficient d'atténuation linéique \(\displaystyle\mathrm{ α_{λ} }\) tel que | \(\displaystyle\mathrm{ A=α_{λ} \ L }\) | |||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||

