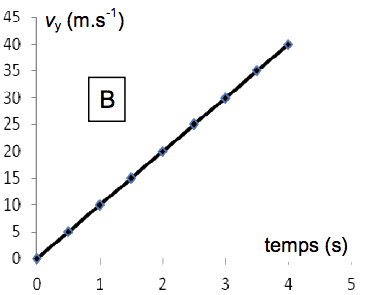|
Démuni des superpouvoirs des supers héros traditionnels, le héros de bande dessinée Rocketeer utilise un réacteur placé dans son dos pour voler. En réalité, ce type de propulsion individuelle, appelé Jet-Pack, existe depuis plus de cinquante ans mais la puissance nécessaire interdisait une autonomie supérieure à la minute. Aujourd’hui, de nouveaux dispositifs permettent de voler durant plus d’une demi-heure.
Données :
- Vitesse du fluide éjecté supposée constante : Vf=2·103 m·s-1
- Masse initiale du système {Rocketeer et de son équipement} : mR = 120 kg (dont 40 kg de fluide au moment du décollage)
- Intensité de la pesanteur sur Terre : g = 10 m·s-2
- Débit massique de fluide éjecté, considéré constant durant la phase 1 du mouvement : \(\displaystyle\mathrm { D_m=\frac{m_f}{Δt} }\) où mf est la masse de fluide éjecté pendant la durée ∆t
- Les forces de frottements de l’air sont supposées négligeables
1. Mouvement ascensionnel de Rocketeer

Digital art gallery
D’après Pour la Science
n° 406 – aout 2011
Afin de tester le potentiel de son nouveau Jet-Pack, Rocketeer réalise quelques essais de mouvements rectilignes ascensionnels verticaux. Le mouvement de Rocketeer est composé de deux phases : phase 1 et phase 2. Au cours de la phase 1, d’une durée ∆t1 = 3,0 s, il passe de l’immobilité à une vitesse v1, vitesse qui reste constante au cours de la phase 2.
1.1. Pour la phase 1, donner la direction et le sens du vecteur accélération \(\displaystyle\mathrm { \vec{a}_G }\) du système. Que dire de l’accélération dans la phase 2 ? Justifier.
Tous les Jet-Packs utilisent le principe de la propulsion par réaction. Lorsqu’un moteur expulse vers l’arrière un jet de fluide, il apparaît par réaction une force de poussée dont la valeur est égale au produit du débit massique de gaz éjecté par la vitesse d’éjection de ces gaz.
1.2. Étude de la phase 1 du mouvement ascensionnel de Rocketeer. On assimile Rocketeer et son équipement à un système noté M dont on néglige la variation de masse (due à l’éjection des gaz) durant la phase 1 du mouvement.
1.2.1. Juste après le décollage, la force de poussée \(\displaystyle\mathrm { \vec{F} }\) est l’une des forces s’exerçant sur le système M. Quelle est l’autre force s’exerçant sur ce système ?
1.2.2. Trois valeurs d’intensité de force de poussée sont proposées ci-dessous (A, B et C). Justifier que seule la proposition C permet le décollage.
A. 800 N ; B. 1200 N ; C. 1600 N
1.2.3. En supposant que la force de poussée a pour valeur 1600 N, montrer que la masse de fluide consommé durant la phase 1 du mouvement est égale à 2,4 kg.
1.2.4. Après avoir déterminé l’accélération de Rocketeer en appliquant la seconde loi de Newton, estimer la valeur v1 de sa vitesse à l’issue de la phase 1.
2. Problème technique
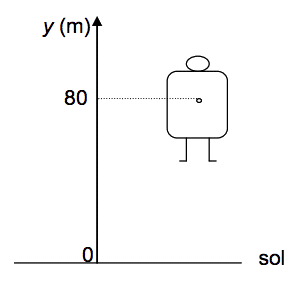
Après à peine quelques dizaines de mètres, le jet-pack ne répond plus et tombe en panne : au bout de 80 m d’ascension verticale, la vitesse de Rocketeer est nulle. Le « Super héros » amorce alors un mouvement de chute verticale. La position de Rocketeer et de son équipement est repérée selon un axe Oy vertical dirigé vers le haut et la date t = 0 s correspond au début de la chute, soit à l’altitude y0 = 80 m. Le schéma ci-contre est tracé sans souci d'échelle.
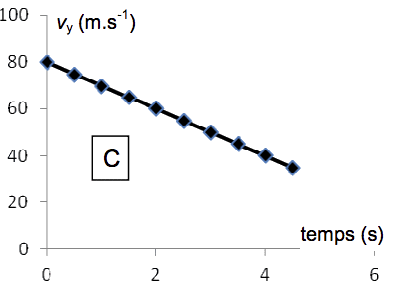
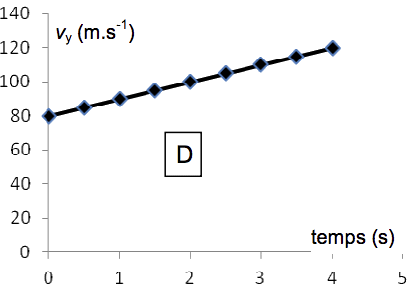
2.1. Les représentations graphiques données ci-après proposent quatre évolutions au cours du temps de Vy, vitesse de Rocketeer suivant l’axe Oy. Quelle est la représentation cohérente avec la situation donnée ? Une justification qualitative est attendue.
2.2. Montrer que lors de cette chute, la position de Rocketeer est donnée par l’équation horaire :
y(t) = -5 t2 + 80 avec t en seconde et y en mètre.
2.3. À quelques kilomètres du lieu de décollage de Rocketeer se trouve le Manoir Wayne, demeure d’un autre super héros, Batman. Alerté par ses superpouvoirs dès le début de la chute de Rocketeer, ce dernier saute dans sa Batmobile, véhicule se déplaçant au sol.

Batman.wikia
Quelle doit être la valeur minimale de la vitesse moyenne à laquelle devra se déplacer Batman au volant de sa Batmobile pour sauver à temps son ami Rocketeer ? Commenter.
|