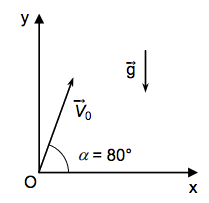Carnet de bac

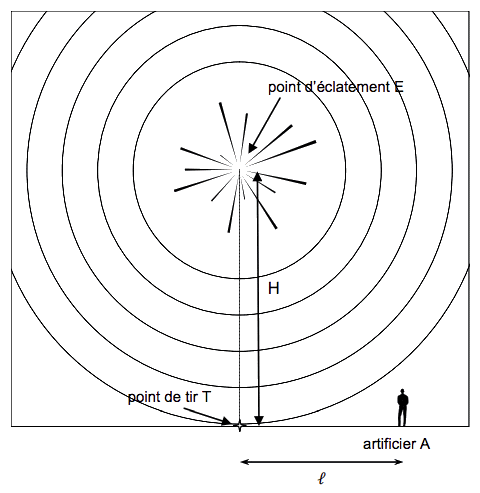
Pour obtenir un feu d'artifice qui produit son, lumière et fumée, on procède à l’éclatement d’une pièce pyrotechnique. Bien que produisant des effets différents, toutes ces pièces sont conçues selon le même principe. Un dispositif permet de projeter la pièce pyrotechnique vers le haut. Une fois que ce projectile a atteint la hauteur prévue par l’artificier, il éclate, créant l’effet « son et lumière » souhaité. Le but de cet exercice est d’étudier la couleur observée, la trajectoire du projectile et le son émis. Les caractéristiques de deux pièces pyrotechniques nommées « crackling R100 » et « marron d’air » sont consignées dans le tableau ci-dessous :

• constante de Planck : h = 6,63·10^-34 J·s
• 1 eV = 1,60·10^-19 J
• échelle des niveaux d’intensité sonore en décibel (dB) et risques auditifs associés

Les feux d’artifice émettent de la lumière. Les phénomènes mis en jeu sont notamment l’incandescence et l’émission atomique. Il y a tout d’abord l’incandescence des particules d’oxyde métallique, formées lors de la combustion, qui va du « blanc rouge » (aux alentours de 1 000 °C) jusqu’au blanc éblouissant (vers 3 000 °C). Pour l’émission atomique, les électrons de l’atome sont excités thermiquement, ce qui leur permet de passer du niveau d’énergie fondamental à un niveau d’énergie supérieur ; au cours de leur retour vers le niveau d’énergie fondamental, l’énergie qu’ils avaient absorbée est émise sous forme de photons dont la longueur d’onde est caractéristique de l’atome.

D’après Ambafrance

1.1. Le texte fait référence à deux processus d’émission de lumière. Citer chacun de ces processus et préciser, dans chaque cas, si le spectre de la lumière émise est un spectre de raies ou un spectre continu. Le « crackling R100 » est principalement composé de strontium. Les photons émis par le strontium sont responsables de la couleur perçue lors de l’éclatement du « crackling R100 ». Le tableau ci-dessous regroupe les énergies des photons émis par le strontium :

1.2. Déterminer la couleur perçue lors de l’émission du photon 3.

1.3. Sans effectuer de calcul supplémentaire, montrer que l’émission de ces trois photons permet d’expliquer la couleur de la lumière émise par le « crackling R100 ».

2. Étude des trajectoires des pièces pyrotechniques

On s’intéresse au mouvement de la pièce pyrotechnique jusqu’à son éclatement dans un référentiel terrestre supposé galiléen muni d’un repère (Ox,Oy). On étudie le mouvement d’un point M de la pièce « crackling R100 ». On prend l’instant du lancement comme origine des temps t = 0 s. À cet instant, le vecteur vitesse initiale \(\displaystyle\mathrm { \overrightarrow{V}_0 }\) de M fait un angle α = 80° par rapport à l’horizontal (schéma ci-contre).

2.1. Etablir l'expression du vecteur \(\displaystyle\mathrm { \overrightarrow{V}_0 }\) en fonction de V₀ et α.

2.2. Etablir les équations horaires du mouvement de M.

2.3. Dans le cadre de ce modèle, déterminer, à l’aide des équations horaires, l’altitude théorique atteinte par le projectile à t = 3,2 s.

2.4. Sachant que l’éclatement se produit lors de la montée, expliquer l’écart entre cette valeur et celle annoncée par le constructeur.

3. Le « marron d’air »

Au début et à la fin de chaque feu d’artifice, les artificiers utilisent une pièce pyrotechnique appelée « marron d’air » pour obtenir une détonation brève et puissante. Désireux de l’envoyer le plus haut possible, ils effectuent un tir vertical avec une vitesse initiale v_i . Par la suite, on suppose que la pièce n’éclate pas avant d’atteindre sa hauteur maximale h.

3.1. Dans l’hypothèse où l’énergie mécanique de la pièce pyrotechnique se conserve, caclucler la hauteur maximale h atteinte par cette pièce.
3.2. Déterminer la valeur de la hauteur maximale atteinte h. En réalité, arrivé à une hauteur H de 70 m, le « marron d’air » éclate au point E et le son émis se propage dans toutes les directions de l’espace. Un artificier A se trouve à la distance ℓ = 95 m recommandée par le constructeur du point de tir T du « marron d’air ».

Remarque : Sur ce schéma, les échelles de distances ne sont pas respectées.

3.3. Doit-on recommander à l’artificier le port d’un dispositif de protection auditive (casque, bouchons d’oreille,…) ? Justifier par un calcul.