Carnet de bac

Le canal de Corinthe est situé en Grèce. Il a été creusé pour relier la mer Égée et la mer Ionienne. Les parois rocheuses sont très hautes et l'eau s'écoule à 79 m au-dessous du niveau du sol. Plusieurs pilotes de moto avaient déjà eu l’intention de franchir le canal de Corinthe, situé en Grèce, mais seul l’Australien Robbie Maddison a réalisé cet exploit en avril 2010. Il a pris son élan pour accélérer sa moto et atteindre la vitesse de 125 km·h^-1. Il a ensuite emprunté une rampe qui lui a permis de franchir le canal, avant d'atterrir de l’autre côté. Le point le plus haut de son vol a dépassé les 95 mètres au-dessus du niveau de l’eau.

Kanal Korinth

Robbie Maddison

Dans cet exercice on se propose de vérifier les informations sur ce saut à l’aide de cette chronophotographie (photos prises à intervalles de temps identiques).

Le référentiel d’étude est le référentiel terrestre, supposé galiléen pendant la durée du saut. Le mouvement de Maddison et sa moto est étudié à l'aide du repère (O, x, y) représenté sur la chronophotographie.

À l’instant de date t = 0, Maddison et sa moto se trouvent à l’origine du repère et quittent le tremplin. Le vecteur vitesse \(\displaystyle\mathrm{ \vec{v}_0 } \) du pilote et de sa moto fait alors un angle α avec l’axe horizontal (Ox) comme indiqué sur la chronophotographie.

L’étude est réalisée dans le cadre d’un modèle de chute libre. Maddison et sa moto sont assimilés à un point matériel de masse supposée constante.

Donnée : intensité du champ de pesanteur terrestre, g = 9,81 u.s.i.

1. Pertinence de l’hypothèse d’une chute libre faite par les élèves

Pour justifier que les frottements sont négligeables devant le poids, on étudie le mouvement de Maddison et de sa moto suivant l’horizontale.

1.1 Montrer que si le poids est la seule force qui s’applique sur Maddison et sa moto le mouvement suivant l’axe (Ox) est uniforme. L’établissement des équations horaires du mouvement n’est pas attendu.

1.2 Sans souci d’échelle, utiliser l’extrait ci-dessous de la chronophotographie pour valider le modèle de chute proposé. Justifier en précisant les mesures réalisées.

En tenant compte de l’échelle des distances, on mesure quelques abscisses des positions occupées par Maddison et sa moto et on calcule la vitesse v_x suivant l’horizontale pour ces positions. On obtient les valeurs ci-après :

2.1 Présenter le résultat de ces mesures sous la forme : \(\displaystyle\mathrm{ v_x= \overline{v}_x ± U(v_x) } \) où \(\displaystyle\mathrm{ \overline{v}_x } \) est la valeur moyenne des N mesures et U(v_x) l’incertitude avec un niveau de confiance de 95%. On donne \(\displaystyle\mathrm{ U(v_x)= k \frac{S_{n-1}}{\sqrt{N}} } \) où S_n-1 = 0,543 m·s ^{– 1} et k = 2,6.

2.2 La vitesse en sortie de tremplin v₀ = 125 km·h^-1 annoncée sur les sites internet est-elle vérifiée, sachant que l’inclinaison en sortie du tremplin vaut α = 33° ?

3. Vérification de la hauteur du saut

En utilisant le modèle de la chute libre et les conditions initiales, on obtient la courbe suivante qui représente la composante suivant y de la vitesse v_y(t) en fonction du temps.

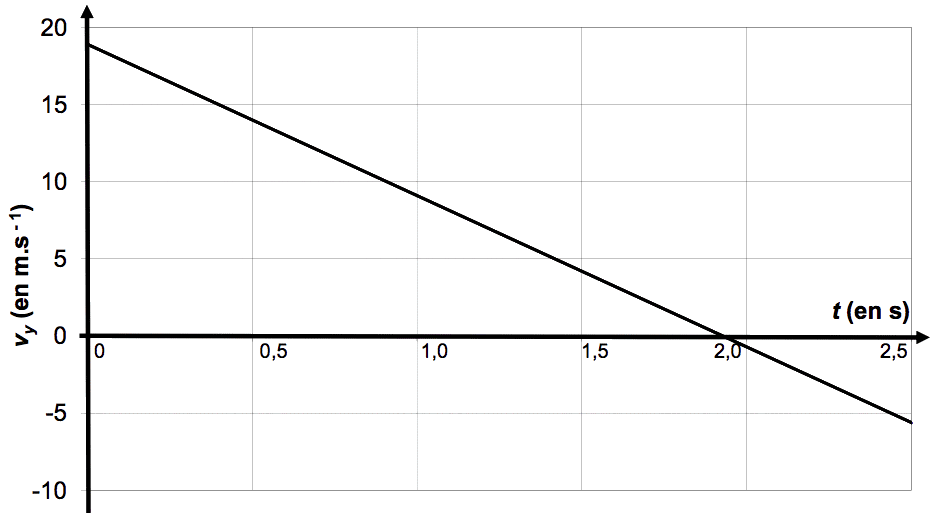
3.1 En utilisant l’allure du graphique v_y(t), justifier que le mouvement suivant la verticale est uniformément varié.

3.2 Quelle position particulière de la trajectoire est occupée par Maddison et sa moto à la date pour laquelle v_y = 0 ? Quelle est alors la valeur de la vitesse à cette date ?

L’énergie potentielle de pesanteur est nulle lorsque y = 0 m.

3.3 Donner l’expression de l’énergie mécanique de Maddison et sa moto en fonction de la masse m, la vitesse v, l’ordonnée y et l’intensité de la pesanteur terrestre g.

3.4 En utilisant l’expression précédente, déterminer l’ordonnée y_S du point S, sommet de la trajectoire.

3.5 Le niveau de l'eau du canal de Corinthe est situé à 79 m au-dessous du niveau du sol. Le point de sortie du tremplin se situe à 5,7 m au-dessus du niveau du sol. Le résultat précédent confirme-t-il l’information suivante : le point le plus haut de son vol a dépassé les 95 mètres au-dessus de l’eau ?