Carnet de bac
Annales
Observation d'une exoplanète |
|
| Antilles 2017 (remplacement) - Exercice 3 - 5 points |
|
L’existence de planètes situées en dehors du système solaire (ou exoplanètes) fait l’objet d’études scientifiques depuis le XIXème siècle. Leur éloignement, mais aussi leur manque de luminosité par rapport aux étoiles autour desquelles elles tournent, rendent leur détection difficile.
| |||
|
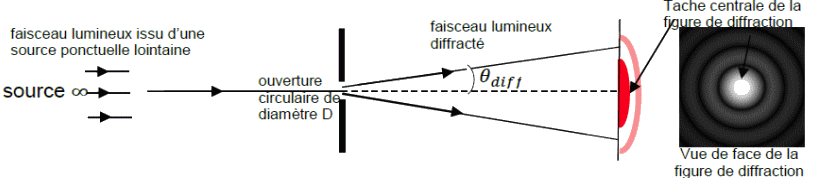
Document 1 - Diffraction par une ouverture circulaire
Dans le cas d’une ouverture circulaire, on admet que l’angle de diffraction θdiff (exprimé en radian)
vérifie la relation \(\displaystyle\mathrm{ θ_{diff}=1,22 \ \frac{λ}{D} } \) , où λ est la longueur d’onde du faisceau incident et D le diamètre de l’ouverture.
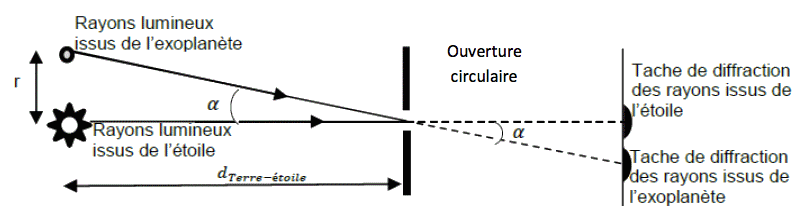
α est l’écart angulaire entre l’étoile et la planète, c’est à dire l’angle sous lequel l’écart angulaire étoile-planète est vue depuis la Terre. Il se calcule grâce à la relation : \(\displaystyle\mathrm{ α=tanα=\frac{r}{d_{Terre-étoile}} } \) où r est la distance entre la planète et l’étoile et dTerre-étoile la distance entre la Terre et l’étoile. Critère de Rayleigh pour distinguer deux objets Un télescope permet de distinguer deux objets à condition que l’écart angulaire α entre ces deux objets soit supérieur ou égal à l’angle de diffraction θdiff.
| |||
Données :
1.1. Quelle propriété de la lumière permet d’expliquer le phénomène de diffraction ?
| |||
|
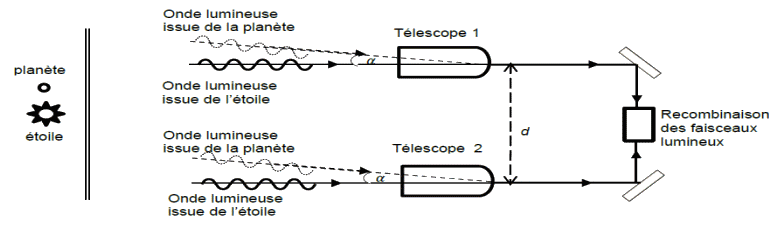
Document 2 - Dispositif interférométrique
On considère deux télescopes identiques dont les lignes de visées sont dirigées vers une étoile lointaine. La direction d’une exoplanète à proximité de l’étoile fait un angle α avec la ligne de visée.
Dans ce dispositif, les faisceaux issus des deux télescopes sont recombinés grâce à un dispositif optique situé à égale distance des deux télescopes. | |||
Recombinaison des signaux issus de l’étoile
|