|
Un cours avec Walter H.G. Lewin ressemble à un spectacle vivant. Personne ne sait véritablement à quoi s'attendre. Le professeur met en scène les expériences. Il y a du suspense... et du risque. Ainsi, il lâche une boule très lourde suspendue à une corde, et reste immobile. Par effet de balancier, elle revient à vive allure, se rapproche dangereusement de son visage, et stoppe alors même qu'on était persuadé qu'il se broierait le nez.
D’après le site Thot ursus (Formation et culture numérique)
Cet exercice utilise des extraits de vidéos afin d’exploiter les expériences réalisées par le professeur Walter H.G.Lewin. Le professeur utilise un pendule simple constitué d’un câble inextensible de masse négligeable, auquel est reliée une boule d’acier pleine et homogène de masse 15 kg et de diamètre 13 cm. Le pendule est accroché au plafond de l’amphithéâtre ; la longueur L entre le plafond et le centre G de la boule est de 5,21 m.
Donnée : valeur de l’intensité du champ de pesanteur terrestre g = 9,81 m·s-2
1. Première expérience

Dans une première expérience, le professeur Walter H.G.Lewin amène la boule contre son menton (photo ci-contre).

Après avoir lâché la boule sans vitesse initiale, à partir d’un angle de 41° par rapport à la verticale, celle-ci fait un aller et retour et s’approche du menton de Walter .G.Lewin, sans toutefois le toucher.
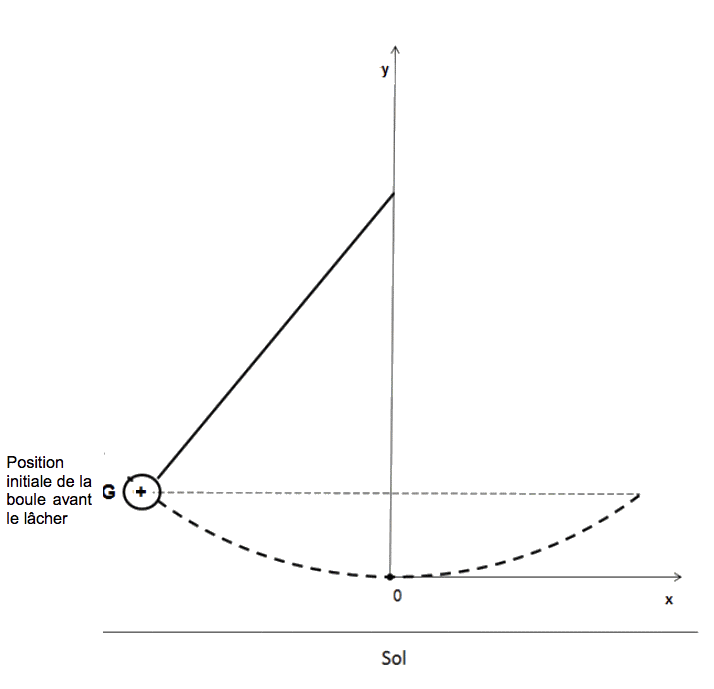
1.1. Compléter le schéma, en annexe à rendre avec la copie, en y reportant les mesures connues de la situation initiale au moment du lâcher. En déduire, par un calcul, l’altitude initiale du centre G de la boule en prenant comme origine celle proposée sur le schéma (ce schéma n’est pas à l’échelle).
1.2. Faire l’inventaire des forces qui s’exercent sur la boule, et les représenter, sans souci d’échelle sur le schéma en annexe à rendre avec la copie. On néglige toutes les forces exercées par l’air.
1.3. Par convention, on pose que l’énergie potentielle de la boule au point O est nulle. Montrer que l’énergie mécanique initiale de la boule est de 1,9·102J.
1.4. Quelle est la position du centre G de la boule correspondant à la vitesse maximale de la boule ?
1.5. Calculer la vitesse maximale, exprimée en km·h-1, atteinte par la boule au cours de cet aller-retour sans frottements.
1.6. En quoi la photographie du document 1 contredit-elle l’hypothèse formulée à la question 1.2. ?
2. Deuxième expérience
Dans une deuxième expérience, le professeur Walter H.G. Lewin réalise deux mesures avec ce même pendule.
2.1. Première mesure : Il écarte le pendule d’un angle de 10° par rapport à la verticale. Il déclenche un chronomètre au moment où il lâche la boule sans vitesse initiale. Il compte avec ses étudiants le nombre de fois où la boule revient quasiment à sa position initiale. À la dixième fois, il arrête le chronomètre qui affiche alors la valeur : 45,81 s. Le chronomètre donne un résultat avec une incertitude de ± 0,2 s. Puis il note au tableau l’indication : 10 T =45,8 ± 0,2 s.
 |  |
La capture d’écran a été réalisée au moment où la boule était dans la position la plus haute (avec une vitesse nulle) après avoir fait un aller-retour. Le cercle en pointillés représente la position de la boule au moment du lâcher.
2.1.1 En utilisant les résultats inscrits au tableau, donner un encadrement de la valeur de la période de ce pendule simple.
2.1.2 Commenter la méthode de mesure utilisée par le professeur.

2.2. Deuxième mesure : Le professeur s’assied ensuite sur la boule (photo ci-contre), et précise qu’il doit se mettre en position allongée pour ne pas fausser la démonstration. Puis, de la même manière, il s’écarte afin que le câble fasse un angle de 10° par rapport à la verticale. Il se laisse ensuite balancer avec la boule et il se filme. La vidéo a ensuite été exploitée pour donner les courbes d’évolution temporelles représentées sur le document 2 ci-dessous.
Document 2 : Exploitation de la vidéo
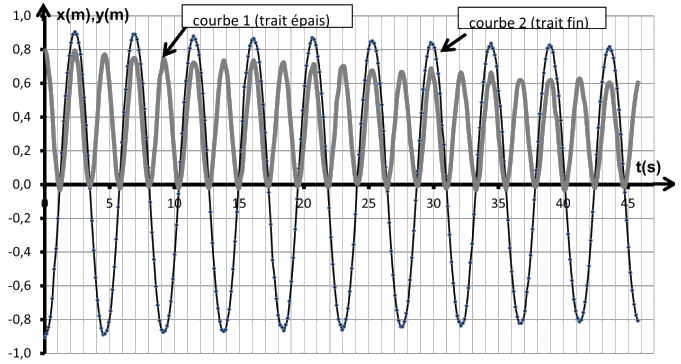
2.2.1. L’une des courbes représente x (t) et l’autre y(t) ; les axes Ox et Oy sont ceux définis sur le schéma de l’annexe, identifier les courbes correspondantes en commentant leur allure.
2.2.2. Déterminer la valeur de la période de ce pendule constitué du câble, de la boule et du professeur.
2.2.3. Par une analyse dimensionnelle, vérifier l’homogénéité de l’expression de la période T du pendule : \(\displaystyle\mathrm{ T = k \ \sqrt{ \frac{L}{g} } } \) où k est une grandeur sans dimension.
2.2.4. Expliquer ce que le professeur a voulu démontrer dans cette expérience. Le résultat obtenu est-il concluant ?
|