Carnet de bac
Annales
Les tirs au buts |
SUP ➔ |
| Antilles 2015 - Exercice 1 - 6 points |
|
Antonin Panenka, footballeur international tchécoslovaque est connu pour avoir laissé son nom à une technique particulière pour tirer les penaltys ou « tirs au but ». Au lieu de frapper en force, il frappe doucement le ballon qui prend alors une trajectoire en « cloche ». Son geste est devenu célèbre au soir de la finale de la Coupe d’Europe des Nations de 1976, où la Tchécoslovaquie battait la République Fédérale d’Allemagne tenante du titre. Antonin Panenka marquant le dernier pénalty par cette technique de balle « en cloche » venait d’inventer la « Panenka ».
1. Schématisation du problème
|
|
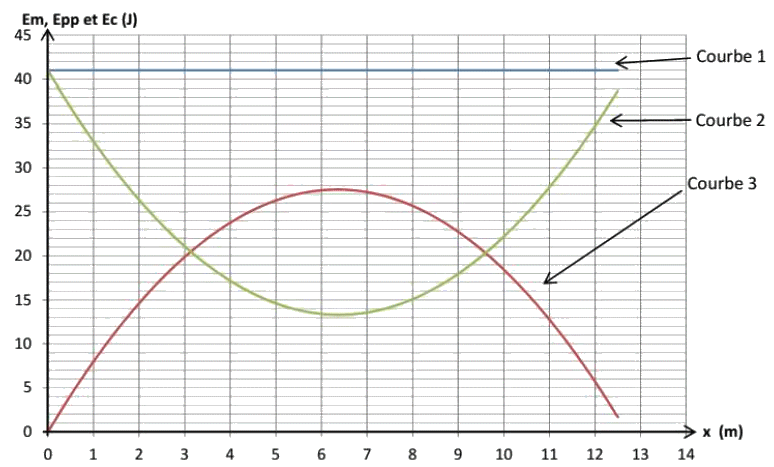
Document 1 : Évolution des énergies Em, Epp et Ec
|