Carnet de bac

Wikipédia

Le VLT (Very Large Telescope) est situé dans le désert d'Atacama au nord du Chili à 2 635 m d'altitude. Il est constitué d’un ensemble de quatre télescopes nommés Antu, Kueyen, Melipal et Yepun ayant des miroirs de 8,2 mètres de diamètre.
L’objectif de cet exercice est de comprendre pourquoi les scientifiques construisent des télescopes ayant des diamètres de plus en plus grands. Les différentes parties sont indépendantes.

Partie 1 : Un télescope du VLT

Lorsqu'on observe une étoile à travers un télescope, l'image apparaît sous la forme d'une tache, dont la dimension est liée aux défauts que présente l'instrument, tels que :
- la sensibilité aux fluctuations atmosphériques ;
- la diffraction par l'ouverture limitée de l'instrument.

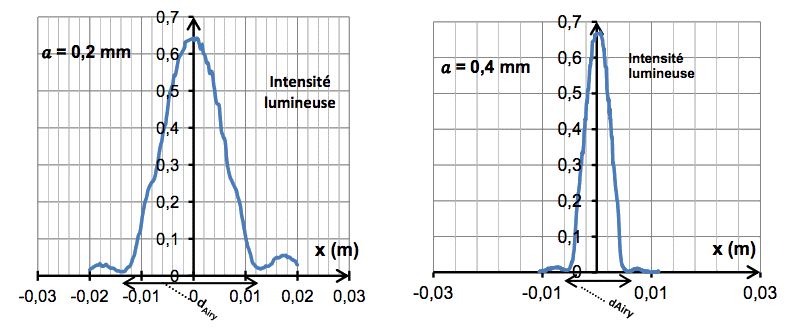
On étudie l’influence du diamètre de l’ouverture circulaire du télescope sur la qualité de l’image formée. Pour cela, on réalise le montage suivant (figure 1), dans lequel le laser correspond à l’étoile et le miroir du télescope est modélisé par une ouverture circulaire de diamètre a produisant un phénomène de diffraction.

Figure 1 : Expérience de diffraction

1.1. Décrire le phénomène de diffraction. Dans quelle condition ce phénomène est-il observable ?

1.2. Quel caractère de la lumière est mis en évidence par l’apparition d’une figure de diffraction ?

1.3. À partir des résultats expérimentaux, déterminer la valeur du diamètre d_Airy de chaque tache observée pour les deux ouvertures. Comment évolue le diamètre de la tache quand l’ouverture du télescope augmente ?

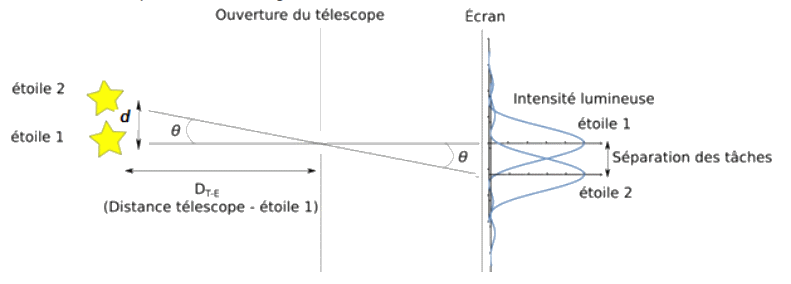
La qualité d’un télescope est caractérisée par son pouvoir de résolution ; c’est-à-dire sa capacité à séparer deux objets très proches comme une étoile double par exemple (images ci-dessous).

Source : Podcast Science

L’observation, par un télescope des deux étoiles, d’une étoile double, séparées d’un angle θ, donne deux taches circulaires sur l’écran si l’angle sous lequel elle sont vues, est supérieur à une valeur limite \(\displaystyle\mathrm{ θ_{min}= 1,22 \frac{λ}{a} } \)

• la distance Terre-Lune est égale à D_T-L = 3,8·10⁸ m ;
• la vision humaine a une sensibilité maximale, en vision diurne, pour un rayonnement de longueur d'onde voisine de 560 nm.

1.4. On considère deux objets placés sur la Lune à une distance d l’un de l’autre. Déterminer la valeur minimale de la distance d pour que les deux objets puissent être séparés par :
- un télescope terrestre de diamètre 4,0 m ;
- un télescope du VLT?

1.5. Au vu des résultats obtenus, justifier les choix des scientifiques en termes de matériel et de leur implantation.

Partie 2 : Entretien des miroirs du VLT

Sean Riley, journaliste pour l’émission Superstructures SOS, suit une équipe internationale d'ingénieurs et astronomes, pour changer le miroir géant d'un des quatre télescopes du VLT. L'ennemi « numéro un » est la poussière et nettoyer la surface du miroir se fait avec une machine spéciale comme un « gros lave-vaisselle ». Le miroir de 50 m² de surface est débarrassé de sa couche d’aluminium de 80 nanomètres d’épaisseur avec de l’eau, de l'acide et du sulfate de cuivre. L'opération consomme environ 3 000 litres d'eau. Il est ensuite recouvert d'une nouvelle fine couche d'aluminium identique à la précédente.

D’après l’émission France 5 Superstructures SOS - Le miroir des étoiles

Données : couples oxydant/réducteur : H3O+(aq)/H2 (g) et Al3+(aq)/Al(s) ; masse volumique de l’aluminium : ρAl = 2,7·106g·m–3; masse molaire atomique : M(Al) = 27 g·mol–1; acide chlorhydrique H3O+(aq) + Cl-(aq) 37 % est le pourcentage massique de l’acide chlorhydrique ; dans 100 g de solution, il y a 37 g d’acide chlorhydrique.

Étiquette du flacon d’acide chlorhydrique utilisé

2.1. Première étape : élimination de la couche d’aluminium

La procédure indique que, pour éliminer l’ancienne couche d’aluminium, on traite le miroir avec une solution d’acide chlorhydrique et de sulfate de cuivre. On fait l’hypothèse que seul l’acide chlorhydrique, attaque l’aluminium. L’action de l’acide chlorhydrique sur l’aluminium peut être modélisée par l’équation suivante :

2 Al_(s) + 6 H₃O⁺ → 2 Al³⁺_(aq) + 3 H_{2 (g)} + 6 H₂O_(ℓ)

2.1.1 À partir des demi-équations électroniques des couples oxydant/réducteur, retrouver l’équation de la réaction entre l’aluminium et les ions oxonium de la solution d’acide chlorhydrique.

2.1.2 De quel type de réaction s’agit-il ? Quel est le rôle de l’aluminium et celui des ions oxonium ? Justifier.

2.1.3 Quel est le volume d’aluminium V_Al déposé sur le miroir ? Vérifier que la quantité de matière d’aluminium présente dans cette couche est égale à n_Al = 0,40 mol.

2.1.4 Déterminer la quantité de matière d’ions oxonium H₃O⁺ nécessaire à l’élimination de la couche d’aluminium.

2.1.5 Montrer que la concentration molaire C_a de la solution d’acide chlorhydrique à 37 % est de l’ordre de 12 mol·L^–1.

2.1.6 La solution d’acide chlorhydrique précédente étant trop concentrée, on souhaite préparer une solution S1 cent fois moins concentrée. Proposer un protocole expérimental pour préparer 1,00 L de la solution diluée.

2.1.7 Quel volume V₁ de la solution S₁ d’acide chlorhydrique est nécessaire pour éliminer la couche d’aluminium ?

2.2. Deuxième étape : dépôt d’une nouvelle couche d’aluminium

Après l’élimination de l’ancienne couche d’aluminium des miroirs des télescopes du VLT, il est nécessaire d’en déposer une nouvelle. L’objectif de cette partie est d’étudier la technique utilisée : la pulvérisation cathodique.

Principe de la pulvérisation cathodique
L’application d’une tension électrique permet la création d’un plasma d’argon état de la matière constituée de particules neutres et chargées) : un électron d’une couche externe de l’atome d’argon Ar peut être arraché lors d’une collision entre un atome d’argon et un électron incident. Ce mécanisme est modélisé par : $$\mathrm{ Ar + e^-_{incident} \rightarrow Ar^+ + e^-_{incident} +e^-_{émis} } $$ Sous l’effet du champ électrique, les ions positifs Ar⁺ du plasma se trouvent attirés par la cathode en aluminium et entrent en collision avec cette dernière, ce qui provoque la pulvérisation des atomes d’aluminium qui vient se déposer sur le miroir.

Données :

• 1 eV correspond à 1,60·10^–19 J ;
• constante de Planck : h = 6,63·10^–34 J·s ;
• masse de l’électron : m = 9,11·10^–31 kg ;
• énergie d’ionisation de l’atome d’argon : E_i = 15,8 eV.

2.2.1 L’énergie nécessaire à l’ionisation de l’atome d’argon est apportée par l’énergie cinétique de l’électron incident. Déterminer la vitesse de l’électron incident. Commenter l’ordre de grandeur obtenu.

2.2.2 Si l’énergie transférée par l’électron incident, lors de la collision, n’est pas suffisante pour l’ionisation, un électron de la couche externe de l’atome d’argon peut passer à un niveau excité. Dans le cas d’un transfert d’énergie de 11,6 eV, faire un schéma énergétique et indiquer par une flèche la transition se produisant. Quelle est la nature du rayonnement (IR, visible, UV) émis par l’électron quand il revient à son état fondamental ?