|
La pétanque est un jeu de boules dérivé du jeu provençal aussi appelé "la longue". Le but du jeu consiste tout simplement à lancer la boule le plus près possible du "but" matérialisé par le bouchon. Le terrain de jeu est horizontal.
Au début d’une partie de pétanque, un joueur trace un cercle sur le sol, il se place dans ce cercle et lance le bouchon à une distance entre 6 et 10 mètres de ce cercle. Les joueurs de pétanque ont le choix entre pointer c'est-à-dire tenter de placer leur boule plus près du but que l’adversaire ou tirer c'est-à-dire déplacer la boule adverse pour l'éloigner du "but" et remporter le point.
Le pointeur joue avec des boules de petit diamètre (71 à 74 mm) pour offrir moins de surface au tireur, assez lourdes pour un meilleur contrôle (710 à 740 g). Le tireur joue avec des boules de gros diamètre (74 à 78 mm), légères afin de limiter la fatigue (670 à 700 g).
D’après La boule bleue.fr
Cet exercice aborde l’étude d’un lancer d’une boule par un pointeur, puis par un tireur. Dans tout
l’exercice, les frottements seront négligés.
Partie A - Le pointeur
Le pointeur lance sa boule de masse m = 710 g avec une vitesse initiale \(\displaystyle\mathrm{ \vec{v}_0 } \) faisant un angle α par rapport à l’horizontale. L’origine O est prise au point où le pointeur lâche la boule. Le modèle de la
chute libre conduit aux équations horaires du mouvement du centre G de la boule dans le repère (O, x, y):
$$\mathrm{ x = V_0 \ t \ cos α } $$
$$\mathrm{ y= - \frac{1}{2} \ g \ t^2 +V_0 \ t \ sin α } $$
1. On réalise la chronophotographie du mouvement de la boule lancée par le pointeur. Cette chronophotographie est représentée ci-dessous ; l’intervalle de temps entre deux prises de vue est de 33,3 ms.

Quelques coordonnées du centre de la boule de pétanque
| Date t (s) |
x (m) |
y (m) |
| 0,000 |
0,000 |
0,000 |
| 0,033 |
0,117 |
0,117 |
| 0,067 |
0,243 |
0,243 |
| 0,100 |
0,346 |
0,360 |
1.1. Déterminer, à partir de la chronophotographie, la valeur de l’angle α entre l’horizontale et le vecteur vitesse à l’origine des dates en précisant la méthode choisie.
1.2. En exploitant le modèle de la chute libre et en utilisant les résultats expérimentaux, déterminer la valeur de la vitesse initiale V0.
2. Le pointeur lance la boule en direction du bouchon et la lâche au point O origine du repère choisi. Le point O est situé à une hauteur de 1,2 m du sol.
2.1. Déterminer l'équation de la trajectoire de la boule.
2.2. Pour un angle α de 51° et une vitesse initiale de valeur égale à 5,5 m·s-1, la boule touche le sol, puis roule vers le bouchon. Calculer l’abscisse du point d’impact de la boule avec le sol.
Partie B - Le tireur
La boule lancée par le pointeur étant proche du bouchon, le tireur de l'équipe adverse va chercher à la déplacer. Le tireur lance sa boule à quelques centimètres de la boule visée ; la boule du tireur roule puis percute la boule du pointeur de plein fouet avec une vitesse V2 = 8,0 m·s-1. Dans le référentiel terrestre, après le choc, les deux boules, de masses respectives m1 et m2, possèdent les vecteurs vitesse \(\displaystyle\mathrm{ \vec{v'}_1 } \) et \(\displaystyle\mathrm{ \vec{v'}_2 } \) portés par la même direction.
On étudie le cas de figure du choc donné par le schéma suivant :
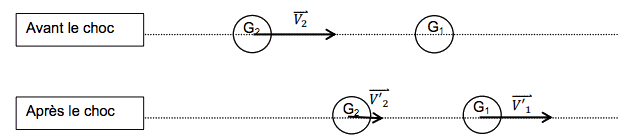
1. L'énergie cinétique et la quantité de mouvement du système constitué par les deux boules sont constantes au cours du mouvement. En déduire les expressions de \(\displaystyle\mathrm{ \vec{V'}_1 } \) et de \(\displaystyle\mathrm{ \vec{V'}_2 } \) en fonction de \(\displaystyle\mathrm{ \vec{V}_2 } \) .
À partir de ces relations vectorielles, associer les relations A, B et C comparant les masses aux trois propositions 1, 2 et 3 :
| m1 = m2 |
A |
|
1 |
la boule G2 repart en sens inverse |
| m1 > m2 |
B |
|
2 |
la boule G2 suit la boule G1 |
| m1 < m2 |
C |
|
3 |
les boules échangent leurs vitesses |
Reporter vos réponses sur votre copie et justifier chaque choix.
2. Que se passe-t-il si la masse m1 est très largement supérieure à la masse m2 ?
|



