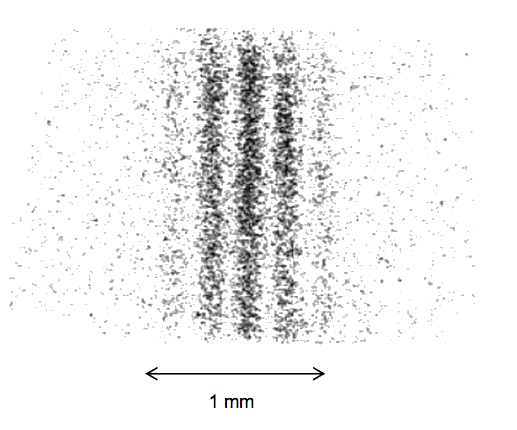Carnet de bac

En 1929, le prix Nobel de physique est attribué au mathématicien et physicien français Louis de Broglie pour sa découverte de la nature ondulatoire des électrons. Ses travaux sont considérés aujourd’hui comme fondateurs de la physique quantique, dont une des lois fondamentales, dite loi de de Broglie, peut s’énoncer de la façon suivante : « À toute particule matérielle de masse m et de vitesse v est associée une onde de matière de longueur d’onde λ $$\mathrm{ λ = \frac{h}{p} } $$ h étant la constante de Planck et p la quantité de mouvement de la particule. »

De nos jours, cette loi est à la base du principe de fonctionnement de certains gravimètres, appareils permettant d’obtenir une valeur très précise de l’intensité de pesanteur. Une application des gravimètres est la détection d’anomalies gravitationnelles permettant d’anticiper la détection de séismes ou de faire de la prospection pétrolière ou archéologique.
Un gravimètre à atomes froids utilise un dispositif vertical dont le principe de fonctionnement simplifié est schématisé ci-dessous. Il utilise des atomes de Néon piégés et refroidis à une température de 2,5 millikelvins. Ces atomes quittent le piège sans vitesse initiale et tombent dans le champ de pesanteur \(\displaystyle\mathrm{ \vec{g} } \) .

Le piège est situé à une hauteur L au-dessus de deux fentes séparées d’une distance d. Un écran de détection est placé à une distance D des deux fentes ; il permet de détecter chaque impact d’atome de Néon.

On obtient sur l’écran de détection une figure d’interférences constituée d’environ 6 impacts d’atomes. Figure d’interférences observée sur l’écran de détection D’après F. Shi izu, K. Shi izu, H. Taku a, Double-slit Interference whith ultracold metastable neon atoms; Physical Rewiew A; 1992.

• Masse d’un atome de Néon m= 3,35·10^-26 g ;
• Constante de Planck : h=6,63·10^-34 J·s ;
• Vitesse des atomes au niveau de la double fente : v_F=1,2 m·s^-1.

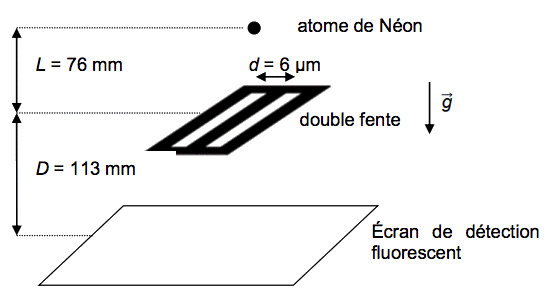
On applique successivement deux modèles mécaniques aux atomes de Néon pour expliquer le fonctionnement du gravimètre.

1. Chute de l’atome avec le modèle de Newton

On utilise la mécanique de Newton pour décrire la chute libre d’un atome de Néon entre le moment où il quitte le piège et celui où il atteint la double fente.

1.1. Montrer que la vitesse d’un atome au niveau de la double fente est verticale et que sa valeur est donnée par la relation : \(\displaystyle\mathrm{ v_F = \sqrt{2 \ g \ L} } \)

1.2. Dans le cadre de la mécanique de Newton, on suppose que les atomes issus du piège arrivent sur les deux fentes avec une vitesse verticale égale à \(\displaystyle\mathrm{ v_F = \sqrt{2 \ g \ L} } \) . Dans cette hypothèse, dessiner sur la copie la répartition d’un grand nombre d’atomes détectés sur l’écran. Un impact sera représenté par un point noir.

2. Le modèle de de Broglie

La figure obtenue sur l’écran du dispositif est une image d’interférences.

2.1. Quel caractère de la matière est ainsi mis en évidence ?

2.2. Quelle relation mathématique lie les grandeurs physiques p, m et v_F au niveau de la fente ? Préciser l’unité de chaque grandeur.

2.3. Montrer que, dans le modèle de de Broglie, la longueur d’onde λ_th associée à un atome de Néon, au niveau de la double fente, est égale à ,6 - .

2.4. À partir du document fourni en annexe à rendre avec la copie, déterminer, avec le plus de précision possible, la valeur de l’interfrange.

2.5. Déterminer, parmi les propositions suivantes, la formule qui permet de calculer l’interfrange à partir des caractéristiques de l’expérience. Préciser la méthode utilisée.

2.6. En déduire la valeur expérimentale de la longueur d’onde de de Broglie, λ_exp, associée aux atomes de Néon.

2.7. Comparer les longueurs d’onde λ_exp et λ_th.

2.8. Analyse des résultats

2.8.1. Après les deux fentes, la mécanique classique ne peut plus être utilisée. Par contre, la gravitation continue de s’exercer après les fentes. Comment évolue la quantité de mouvement associée aux atomes de Néon entre la double fente et l’écran ?

2.8.2.Comparer qualitativement la longueur d’onde associée aux atomes de Néon au niveau de la double fente et au niveau de l’écran.

2.8.3. À quelle longueur d’onde aurait-on dû comparer la longueur d’onde obtenue expérimentalement ?

Détermination de l’interfrange