Carnet de bac
Annales
Quelle teneur en cuivre dans une pièce de cinq centimes d'euros ? |
➔ |
| Antilles 2014 (remplacement) - Exercice 1 - 5 points |
|
La pièce de cinq centimes d’euro est composée d’un centre en acier (constitué essentiellement de fer et de carbone) entouré de cuivre. Elle a un diamètre de 21,25 mm, une épaisseur de 1,67 mm et une masse de 3,93 g. On cherche par une méthode spectrophotométrique à déterminer la teneur en cuivre d’une telle pièce.
3 Cu(s) + 8 H+(aq) + 2 NO3-(aq) → 3 Cu2+(aq) + 4 H2O(ℓ) + 2 NO(g)
3.1. Déterminer, grâce aux valeurs trouvées par les élèves, l’incertitude élargie (pour un niveau de confiance de 95 %) sur la mesure de la masse de cuivre dans une pièce.
| ||||||||||||||||||||||
|
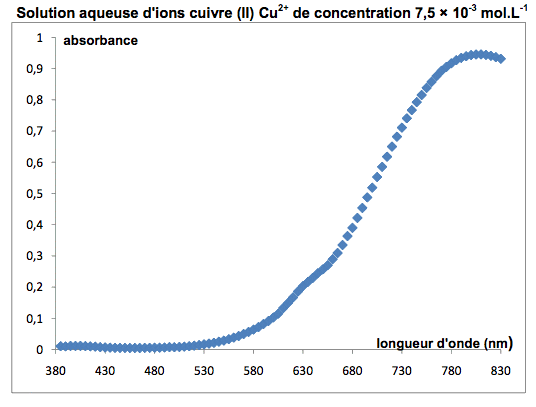
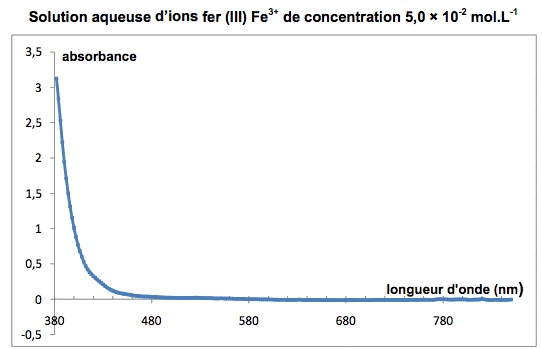
Document 1 : Spectres d’absorption des ions cuivre (II) et fer (III) dans l’eau
On donne ci-dessous les spectres d’absorption d’une solution d’ions cuivre (II) et d’une solution d’ions fer (III), ainsi qu’un tableau reliant longueur d’onde d’absorption et couleur complémentaire. Le « blanc » a été fait avec de l’eau pure.
|
||||||||||||||||||||||
|
Document 2 : Courbe d’étalonnage
Tableau donnant l’absorbance A à 800 nm de solutions aqueuses contenant des ions cuivre (II), obtenues à partir de divers échantillons de métal cuivre pur :
|
||||||||||||||||||||||
|
Document 3 : Incertitude sur un mesurage
On rappelle les différentes formules intervenant dans la détermination de l‘incertitude sur le résultat du mesurage d’un ensemble de n valeurs {x1, x2 … xn} : Écart-type : \(\displaystyle \mathrm{ σ_{n-1}=\sqrt{\frac{\sum_{i=1}^n(x_i-\bar{x})^2}{n-1}} } \) Incertitude-type sur la moyenne : \(\displaystyle \mathrm{ u( \bar{x}) = \frac{σ_{n-1}}{\sqrt{n}} } \) Incertitude élargie sur la moyenne : ,\(\displaystyle \mathrm{ U( \bar{x}) = k \ u( \bar{x}) } \) avec :
|
||||||||||||||||||||||