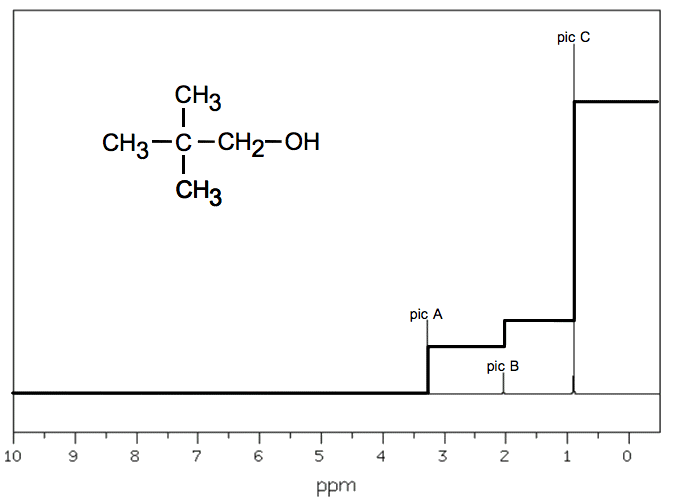Carnet de bac
Annales
RMN et IRM |
➔ |
| Nouvelle-Calédonie 2013 - Exercice 1 - 6 points |
|
La spectroscopie par résonance magnétique nucléaire ou RMN consiste à soumettre une espèce chimique à une onde électromagnétique radiofréquence et à l’action d’un champ magnétique constant. À une fréquence particulière appelée fréquence de résonance, certains noyaux de l’espèce chimique vont être le siège d’une transition énergétique. Les effets de cette transition sont détectés par une sonde.
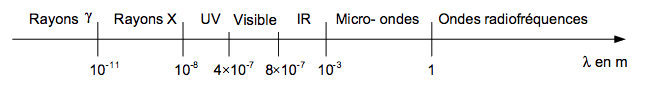
1. RMN du proton dans une molécule organique
1.3.1. Donner le nom systématique (nomenclature officielle) de la molécule organique. 1.3.2. Exploiter le spectre RMN et sa courbe d’intégration pour attribuer à chaque pic son groupe de protons équivalents. 2. L’imagerie par résonance magnétique (IRM) 2.1. Pourquoi l’IRM permet-elle de visualiser les organes et tissus mous, mais pas les os ? 2.2. Image numérique L’image numérique de l’IRM correspond à un ensemble de 512 pixels x 512 pixels où chaque pixel est codé par un octet. La taille de l’image de cet IRM correspond à un carré de 50 cm de côté. 2.2.1. Calculer les dimensions d’un pixel. 2.2.2. Calculer la taille du fichier en octet de cette image IRM. 2.2.3. Combien de niveaux de gris sont utilisés pour visualiser cette image IRM ? 2.2.4. Une image IRM est réalisée toutes les deux secondes. Calculer le débit binaire D permettant de transmettre les données au dispositif de traitement et de stockage. 2.3. Mesure du champ magnétique Un teslamètre est utilisé pour mesurer le champ magnétique créé par l’électroaimant. On a relevé la mesure suivante : Bm = 1492 mT. La notice du teslamètre indique : |
||||||||||
|
- Calibres : 200 mT ou 2000 mT
- Précision : ± (2 % de la mesure + 5 unités de résolution) - Résolution : 0,1 mT pour le calibre 200 mT ou 1 mT pour le calibre 2000 mT |
||||||||||
|
Pour un intervalle de confiance de 95 %, l’incertitude U élargie est donnée par l’expression \(\displaystyle \mathrm{ \frac{2 \times precision}{\sqrt{3}} }\)
|
||||||||||