Carnet de bac

Des protons énergétiques sont des protons animés d’une grande vitesse.

Le but de cet exercice est d’exploiter des documents relatifs à deux exemples de l’action de protons énergétiques sur la matière : le rayonnement cosmique et la protonthérapie.

Données :

• Charge électrique du proton : e = 1,602·10^-19 C
• Masse du proton : m_p = 1,673·10^-27 kg
• Mégaélectron-volt : 1 MeV = 1,602·10^-13 J
• Vitesse de la lumière dans le vide : c = 3,00·10⁸ m·s^-1
• Constante de Planck : h = 6,62·10^-34 J·s

1. Le proton

Dans un noyau atomique, trois interactions fondamentales sont mises en jeu entre les nucléons (protons et neutrons) : l’interaction gravitationnelle, l’interaction électrique et l’interaction nucléaire forte. L’interaction gravitationnelle est attractive ; dans un noyau, elle est nettement plus faible que l’interaction électrique répulsive entre protons. C’est l’interaction nucléaire forte qui assure la cohésion du noyau atomique.

Le proton est composé de trois particules : deux quarks up et un quark down. Les quarks sont des particules élémentaires qui portent une fraction de la charge électrique du proton. La charge d’un quark down est \(\displaystyle\mathrm{ - \frac{e}{3} } \).

1.1. L’interaction forte est-elle attractive ou répulsive ? Est-elle plus ou moins intense que l’interaction électrique ? Justifier vos réponses à l’aide du document 1.

1.2. Déterminer la charge électrique d’un quark up en l’exprimant sous la forme d’une fraction de la charge e du proton.

2. Les protons cosmiques

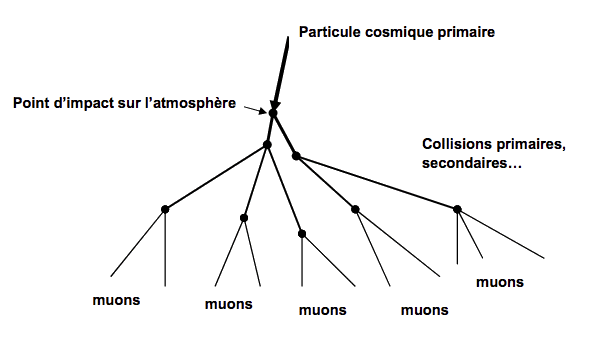
La Terre est arrosée constamment par une pluie de particules, nommée rayonnement cosmique. Ce phénomène est le résultat de l’arrivée de particules énergétiques (provenant du Soleil, de la galaxie et plus globalement de tout l’Univers) dans la haute atmosphère terrestre. Ces particules, principalement des protons (87 %) entrent en collision avec les noyaux des molécules de l’atmosphère. Les produits de ces collisions primaires heurtent à leur tour d’autres noyaux produisant ainsi une gerbe de particules secondaires. Certaines parviennent jusqu’au sol, d’autres sont absorbées par l’atmosphère, et d’autres encore induisent de nouvelles réactions qui donneront naissance à des particules tertiaires, etc… Une seule particule cosmique très énergétique peut générer une gerbe contenant plusieurs milliards de particules (voir figure 1). Plusieurs types de particules atteignent le sol. Parmi ces particules on trouve les muons.

Figure 1 : Représentation simplifiée des gerbes issues de rayonnements cosmiques

On peut appliquer avec une bonne approximation les lois de la mécanique classique, à toute particule animée d’une vitesse inférieure à 10 % de la célérité de la lumière dans le vide, et utiliser l’expression de l’énergie cinétique \(\displaystyle\mathrm{ E_C= \frac{1}{2} \ m \ v^2 } \). Lorsqu’on est dans cette situation, la particule est dite « classique ». Dans le cas contraire, la particule est dite « relativiste ». Par exemple, les protons les plus énergétiques des rayons cosmiques sont relativistes. Ils sont d’origine extrasolaire et leur énergie cinétique est typiquement comprise en 100 MeV et 10 GeV.

2.1. Calculer, en joule puis en mégaélectron-volt, l’énergie cinétique d’un proton animé d’une vitesse égale à 10 % de la célérité c de la lumière dans le vide.

2.2. Justifier par un argument quantitatif la phrase du document 4 : « …les protons les plus énergétiques des rayons cosmiques sont relativistes. »

2.3. D’après la théorie de la dualité onde-corpuscule, que l’on doit au scientifique Louis de Broglie, on associe une onde électromagnétique au proton.

2.3.1. Calculer la valeur de la quantité de mouvement p d’un proton dont la vitesse vaut 10 % de c.

2.3.2. En déduire la valeur de la longueur d’onde λ associée.

3. Les muons

Les muons sont des particules élémentaires voisines de l’électron mais beaucoup plus massives. Ceux qui sont observés au niveau du sol sont créés dans la haute atmosphère à 20 km d’altitude, lors de la collision de protons (appartenant au rayonnement cosmique) avec les noyaux des atomes de l’atmosphère (voir figure 1). Ils voyagent à une vitesse de valeur très élevée (v = 0,9997c). Pour un observateur terrestre, 67 µs sont nécessaires aux muons pour traverser l’atmosphère et atteindre le sol. Or, les muons sont très instables et diverses expériences ont montré que leur durée de vie propre n’est que ∆t₀ = 2,2 µs. Cette durée de vie est donc a priori insuffisante pour leur permettre d’atteindre la surface de la Terre.
Pourtant des muons sont effectivement détectés au niveau du sol. Cette apparente contradiction s’explique par la dilatation des durées dans le cadre de la théorie de la relativité restreinte. En effet, la durée de vie des muons ∆t mesurée sur Terre et la durée de vie propre des muons ∆t₀ qui se déplacent par rapport à la Terre ont des valeurs différentes. Ces deux durées sont liées par la relation de dilatation des durées \(\displaystyle\mathrm{ Δt= γ \ Δt_0 } \) avec \(\displaystyle\mathrm{ γ = \frac{1}{\sqrt{1-\frac{v^2}{c^2}}} } \)

3.1. Expliquer pourquoi les muons sont des particules relativistes.

3.2. Expliquer par un raisonnement quantitatif pourquoi des muons issus des rayons cosmiques peuvent être observés au niveau du sol terrestre.

La radiothérapie (thérapie par rayonnement) est un moyen de traitement du cancer dans lequel les cellules cancéreuses sont détruites par un rayonnement. Si ce rayonnement est électromagnétique (rayons X ou rayons gamma), on parle de photonthérapie. S’il s’agit d’un faisceau de protons, on parle de protonthérapie.
Lorsqu’un rayonnement (photon X ou gamma, proton…) pénètre dans un tissu, il interagit avec celui-ci en lui cédant tout au long de son trajet une part de son énergie, on parle d’énergie déposée. Dans l’exemple du traitement d’une tumeur dans un organisme, le graphique de la figure 2 représente la manière dont évolue l’énergie déposée en fonction de la profondeur de pénétration, d’une part pour un faisceau de photons X ou gamma, et d’autre part pour un faisceau de protons de 150 MeV.
Le faisceau de photons est fortement absorbé dès son entrée dans l’organisme et continue de céder progressivement son énergie tout au long de son parcours. Au contraire, les protons déposent relativement peu d’énergie au début de leur parcours dans l’organisme. L’énergie libérée augmente progressivement au fur et à mesure que leur vitesse diminue. C’est au moment de leur arrêt que l’énergie libérée est maximale. Il apparaît alors un pic de dose (le pic de Bragg), au-delà duquel la dose chute brutalement à zéro.
Tout l’art de la radiothérapie consiste à administrer une dose suffisante pour détruire sans exception toutes les cellules cancéreuses. En revanche cette dose doit endommager le moins possible les cellules saines.

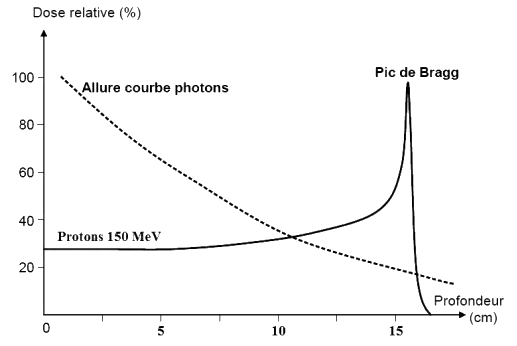
Figure 2 : Énergie déposée dans un tissu en fonction de la profondeur de pénétration du faisceau.

La dose relative est l’énergie déposée par unité de masse de matière, exprimée en pourcentage par rapport au maximum d’énergie qui peut être déposée.