Carnet de bac

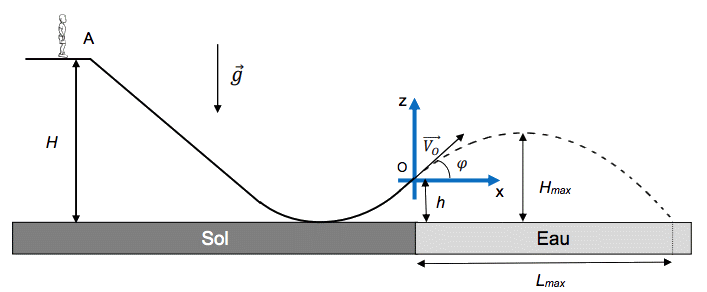
Le water jump est une activité en plein essor. Le principe en est simple : un skieur muni d’une combinaison glisse sur un toboggan préalablement mouillé et terminé par un tremplin. Puis, à la sortie de ce dernier, il effectue un saut en chute libre avant de terminer sa course dans un plan d’eau. Le water jump est également utilisé l’été par les skieurs qui ne peuvent s’entraîner sur les pistes faute de neige.

Données :

• Intensité du champ de pesanteur terrestre : g = 9,81 m·s^-2.
• Masse du skieur et de son équipement : m = 73 kg.

Il existe quatre tremplins dont les caractéristiques sont données dans le tableau ci-dessous.

Le sol horizontal est choisi comme origine de l’énergie potentielle de pesanteur. Les dimensions du skieur étant faibles devant toutes les autres utilisées dans le problème, il est modélisé par un point matériel. Les frottements seront négligés dans toutes les étapes du mouvement.

L’étude est effectuée dans le référentiel terrestre supposé galiléen. L'origine des énergies potentielles est choisie au niveau du sol.

Partie 1 : étude énergétique du skieur sur le tremplin

1.1. Par des mesures, estimer l’angle φ du tremplin photographié de profil.

1.2. S’agit-il du tremplin débutant ou expert ?

1.3. Quel est l’intérêt d’humidifier le toboggan avant son utilisation ?

Utilisation du tremplin débutant
1.4. Exprimer l’énergie mécanique Em_A du skieur à l’instant initial, lorsqu’il s’élance du point A sans vitesse initiale.

1.5. Déterminer la relation entre l’énergie mécanique Em_O au moment où il quitte la piste en O et l’énergie mécanique Em_A. Justifier votre réponse.

1.6. Déterminer la vitesse du skieur au point O.

Utilisation du tremplin médian
1.7. Le skieur s’élance à présent depuis le tremplin médian. Expliquer qualitativement comment varie son énergie mécanique par rapport à la situation précédente.

1.8. Peut-on affirmer que la vitesse du skieur à la sortie du tremplin double lorsque la hauteur du toboggan double ? Justifier qualitativement votre réponse.

Partie 2 : étude du mouvement du skieur après avoir quitté le tremplin

2.1. En détaillant votre raisonnement et en précisant la loi utilisée, exprimer le vecteur accélération \(\displaystyle\mathrm{ \overrightarrow{a} } \) du skieur lorsqu'il a quitté le toboggan.

2.2. On déclenche le chronomètre lorsque le skieur est au point O. Déduire de la question précédente que les équations horaires du mouvement, dans le repère (O,x,z), peuvent s’écrire : $$\mathrm{ x(t)= v_0 \ t \ cosφ } $$ $$\mathrm{ z(t)=-\frac{1}{2} g \ t^2 + v_0 \ t \ sinφ } $$

Partie 3 : application à l’entraînement pour les skieurs durant l’été

En ski acrobatique (« free style »), il faut effectuer un maximum de figures lors des sauts. Pour ce faire les skieurs doivent sauter le plus haut possible.

3.1. Que vaut la composante de la vitesse du skieur suivant z lorsqu’il atteint son point culminant ?

3.2. Le skieur atteint sa hauteur maximale à l'instant t_max. Exprimer t_max en fonction de v_O, g et φ.

3.3. À l’aide des équations horaires, montrer que l’expression de l’ordonnée correspondante, notée z_max dans le repère (O,x,z), vaut \(\displaystyle\mathrm{ z_{max}= \frac{v_0^2 \ sin^2φ }{2 \ g} } \)

3.4. Calculer la hauteur maximale atteinte H_max au-dessus du plan d’eau si le skieur utilise le « tremplin averti » sachant que sa vitesse en O vaut v_O = 5,9 m·s^-1.

3.5. Vous êtes entraîneur d’une équipe de ski acrobatique. Choisir le tremplin à utiliser pour que les skieurs fassent un maximum de figures en vol. Justifier votre réponse à l’aide de l’expression de z_max établie à la question 2.