Carnet de bac

Le 14 octobre 2012, Félix Baumgartner a réalisé un saut historique en inscrivant trois records à son tableau de chasse : celui de la plus haute altitude atteinte par un homme en ballon soit 39 045 m d’altitude, le record du plus haut saut en chute libre, et le record de vitesse en chute libre soit 1341,9 km·h^-1. Après une ascension dans un ballon gonflé à l’hélium, il a sauté vers la Terre, vêtu d’une combinaison spécifique en ouvrant son parachute au bout de 4 min et 20 s. Le saut a duré en totalité 9 min et 3 s.

Ascension du ballon
Il a fallu concevoir un ballon déformable gigantesque, faisant 100 m de hauteur et 130 m de diamètre lors de son extension maximale. En raison de la diminution de la densité de l’air avec l’altitude, le volume du ballon augmente lors de l’ascension de façon à ce que la poussée d’Archimède reste constante. « Pour assurer une vitesse d’ascension suffisante, le volume initial d’hélium utilisé était de 5100 mètres cubes, c’est-à-dire le double du nécessaire pour la sustentation (1). En pratique, si l’on ajoute à la masse de l’équipage celle du ballon et de l’hélium, c’est environ 3 tonnes qu’il a fallu soulever. »

D’après un article de Pour la Science janvier 2013

(1) Sustentation : état d’un corps maintenu à faible distance au-dessus d’une surface, sans contact avec celle-ci.

Étude du saut de Felix Baumgartner
La masse de Félix Baumgartner et de son équipement est m = 120 kg.
La date t = 0 correspond au début du saut de Felix Baumgartner.

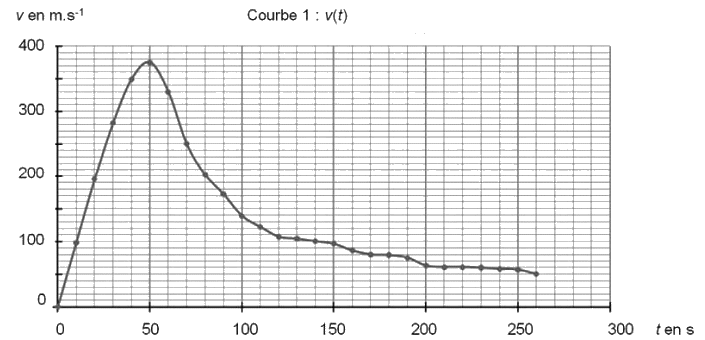
Courbe 1 : évolution temporelle de la vitesse v de Félix Baumgartner, dans le référentiel terrestre, jusqu’à l’ouverture du parachute.

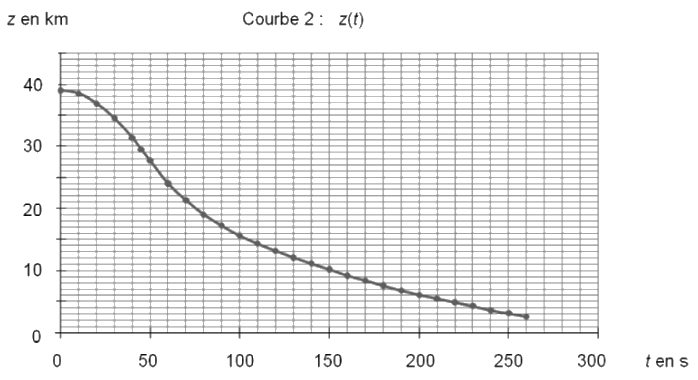
Courbe 2 : évolution temporelle de l’altitude z par rapport au sol de Félix Baumgartner, jusqu’à l’ouverture du parachute.

D’après Dailymotion

Données :

• l’expression de la poussée d’Archimède exercée par l’air sur un corps est la suivante : \(\displaystyle\mathrm { \vec{F}_A= ρ_{air} \ V \ g \ \vec{u}_z }\) avec \(\displaystyle\mathrm { \vec{u}_z }\) vecteur unitaire vertical vers le haut, ρ_air (kg·m^-3) masse volumique de l’air dans lequel est plongé le corps, V (m³) volume du corps placé dans l’air et g intensité du champ de pesanteur
• l’intensité du champ de pesanteur est considérée comme constante entre le niveau de la mer et l’altitude de 39 km : g = 9,8 m·s^-2
• la stratosphère est la couche de l’atmosphère qui s'étend de 10 à 50 km d’altitude environ
• la masse volumique de la partie supérieure de la stratosphère est de l’ordre de 0,015 kg·m^-3, celle de la troposphère au niveau du sol est 1,22 kg·m^-3
• la célérité du son dans l’air en fonction de l’altitude est donnée dans le tableau ci-dessous :
  

  Altitude (km)	10	20	30	40
  Célérité du son (m·s-1)	305	297	301	318

• la vitesse d’un mobile dans un fluide est dite supersonique si elle est supérieure à la célérité du son dans ce fluide

Partie 1 : ascension en ballon sonde de Félix Baumgartner

Le volume de l’équipage est négligeable par rapport au volume du ballon.

1.1. Indiquer la force qui est responsable de l’ascension du ballon.

1.2. Faire le bilan des forces qui s’exercent sur le système {ballon ; équipage} juste après le décollage, en négligeant les forces de frottement. Illustrer ce bilan de forces par un schéma, sans souci d’échelle mais cohérent avec la situation physique.

1.3. En utilisant les données, les informations du texte et les connaissances acquises, vérifier par un calcul que le ballon peut décoller.

1.4. Après quelques minutes d’ascension, le mouvement du système {ballon ; équipage} est considéré comme rectiligne uniforme. Déterminer alors la valeur de la force de frottement de l’air.

Partie 2 : saut de Félix Baumgartner

On étudie maintenant le système {Félix Baumgartner et son équipement} en chute verticale dans le référentiel terrestre considéré comme galiléen. On choisit un axe (Oz) vertical vers le haut dont l’origine O est prise au niveau du sol. Le système étudié, noté S, a une vitesse initiale nulle. On négligera la poussée d’Archimède.

2.1. Utiliser l’étude du saut de Félix Baumgartner (courbe 1) afin de déterminer la valeur de son accélération si t < 20 s. Commenter le résultat obtenu.

2.2. Lors de son saut, Félix Baumgartner a-t-il atteint une vitesse supersonique ? Justifier.

2.3. Calculer la variation d’énergie mécanique ΔE_m entre le moment où Félix Baumgartner saute et le moment où il atteint sa vitesse maximale. Interpréter le résultat.

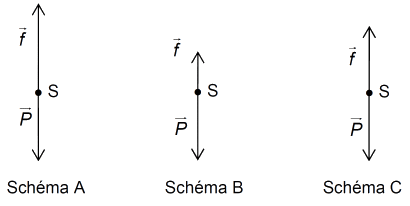
2.4. Les schémas ci-dessous représentent à trois instants les forces appliquées au système S lors du saut : le poids \(\displaystyle\mathrm { \vec{P} }\) et la force \(\displaystyle\mathrm { \vec{f} }\) modélisant les frottements. Affecter un schéma à chacune des dates : t₁=40s, t₂=50s et t₃=60s.

2.5. Déterminer l’altitude à laquelle Félix Baumgartner ouvre son parachute. En supposant que le système a un mouvement rectiligne et uniforme après l’ouverture du parachute et jusqu’à l’arrivée au sol, déterminer la valeur de la vitesse du système durant cette phase du mouvement. On rappelle que le saut a duré en totalité 9 min et 3 s.

2.6. Pour acquérir la même vitesse à l’arrivée au sol, de quel étage d’un immeuble Félix Baumgartner aurait-il dû sauter ? Commenter.