|
Les parties 1, 2 et 3 sont indépendantes.
Les LiDAR, acronyme de « Light Detection And Ranging » sont des systèmes de mesure à distance utilisant généralement les propriétés laser. On les utilise pour la télémétrie (distance Terre-Lune par exemple), la topographie (réalisation de cartes), les mesures de concentrations
de gaz ou encore pour déterminer la vitesse des vents.
Données à 25°C :
| Célérité en m·s-1 | Dans l’air | Dans l’eau |
| onde sonore et ultrasonore : | 3,40·102 | 1,48·103 |
| onde électromagnétique : | 3,00·108 | 2,26·108 |
Constante de Planck : h = 6,62·10–34 J·s
1. Le LiDAR topographique embarqué
Un LiDAR topographique envoie des impulsions laser de courte durée et de longueur d’onde λ = 1064 nm. Tout obstacle sur le trajet du faisceau va renvoyer une partie du rayonnement dans la direction du faisceau incident. La mesure de la durée de l’aller-retour de chaque impulsion permet alors de reconstituer numériquement l’espace environnant. Embarqué à bord d’un avion ou d’un satellite, le LiDAR topographique est un moyen de cartographier la Terre à distance avec une grande précision.
D’après La physique en applications R. Carpentier et B.Depret.
Un des lasers utilisés est un laser dont le milieu amplificateur est un cristal solide néodyme-YAG décrit dans le document n°1 ci-dessous :
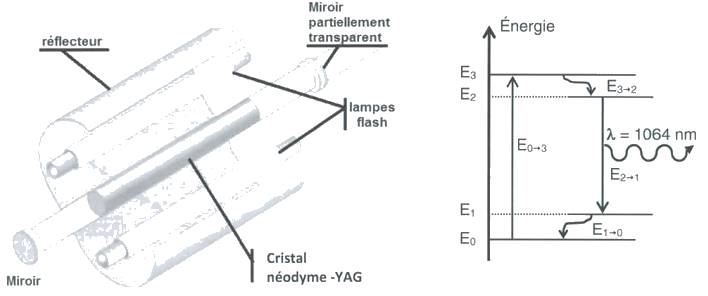
Document n°1 : schéma du laser néodyme-YAG et de son diagramme énergétique simplifié.
1.1. Donner deux propriétés caractéristiques du rayonnement émis par un laser.
1.2. À quoi servent les lampes flash lors du fonctionnement de ce laser ?
1.3. Le niveau fondamental d’énergie E0 est pris comme origine des énergies. L’énergie du niveau E3 est égale à 2,458·10–19 J. Quelle longueur d’onde doit être présente dans le spectre de la lumière émise par une lampe flash ? Sur la figure ci-dessous, l’avion embarquant le lidar topographique vole à une altitude H = 3,50 km à la vitesse de 450 km·h-1. Sa position est déterminée par un GPS.
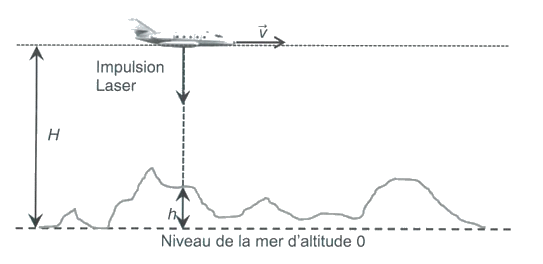
1.4. En faisant l’hypothèse que la distance parcourue par l’avion pendant la durée ∆t est négligeable par rapport à H, montrer que la durée ∆t du trajet aller-retour de l’impulsion laser en fonction de H, h et de la célérité de la lumière c est \(\displaystyle\mathrm { Δt= \frac{2 \ (H-h)}{c}}\).
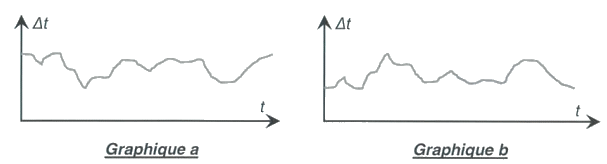
1.5. Parmi les deux graphiques ci-dessous, indiquer celui qui correspond à la situation étudiée. Justifier brièvement la réponse.
1.6. Lors du survol du Puy de Dôme (volcan du centre de la France), on mesure ∆t = 13,6 µs. Estimer l’altitude du Puy de Dôme par rapport au niveau de la mer.
1.7. Dans le cas de la mesure de l’altitude du Puy de Dôme, l’hypothèse faite à la question 1.4. est-elle vérifiée ?
2. Le LiDAR bathymétrique
Les systèmes LiDAR bathymétriques aéroportés ressemblent au LiDAR topographique mais ils sont constitués de deux lasers différents : un laser infrarouge et un laser vert. Ils servent à déterminer la profondeur de l’eau. Pour cela, le LiDAR envoie deux impulsions simultanées (une impulsion verte et une impulsion infrarouge). Le rayonnement infrarouge sert à repérer la surface de l’eau. Le rayonnement vert, quant à lui, pénètre dans l’eau et est réfléchi par le fond. En mesurant la différence entre les temps de parcours des deux impulsions laser (Document n°2), on peut déterminer la profondeur de l’eau.
D’après : Wikhydro
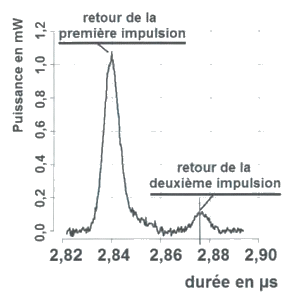
Document n°2
Puissance lumineuse reçue
en fonction du temps | 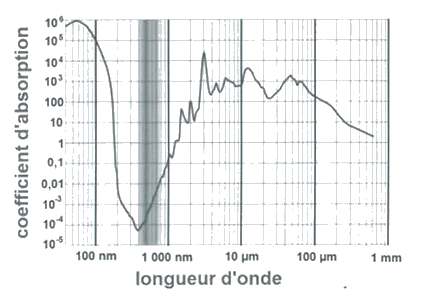
Spectre n°1 : spectre d'absorption de l'eau
La radiation est d'autant plus absorbée que le coefficient d'absorption est élevé. |
2.1. Les longueurs d’onde des deux lasers sont de 532 nm et de 1064 nm. Attribuer, en justifiant, la longueur d’onde à chacun des deux lasers du LiDAR bathymétrique.
2.2. Expliquer pourquoi il est plus judicieux d’utiliser le laser vert, plutôt que le laser infrarouge, pour détecter le fond de l’eau.
2.3. En vous appuyant sur un schéma expliquant le principe de cette mesure, estimer la valeur de la profondeur de l’eau à l’endroit où la mesure du document n°2 a été effectuée.
3. Le LiDAR à effet Doppler
Il permet de faire des mesures de la vitesse de vents ou de nuages grâce à l’effet Doppler. Pour présenter ce principe, un professeur propose le dispositif expérimental photographié ci-après dans lequel le LiDAR est remplacé par un ensemble « émetteur − récepteur » d’ultrasons et le nuage est modélisé par une plaque fixée sur un chariot mobile. On suppose que la température de la salle est de 25°C.
Photographie du dispositif expérimental :

À l’aide de ce dispositif, le professeur a proposé aux élèves de réaliser deux expériences pour mesurer la vitesse de déplacement d’un objet.
Expérience n°1
Pour déterminer la valeur v de la vitesse de déplacement du chariot, Anna, à l’aide d’un chronomètre, mesure la durée mise par le chariot pour se déplacer d’une distance d = 30,0 ± 0,5 cm. Elle réalise plusieurs chronométrages dont les résultats sont regroupés dans le tableau suivant :
| Mesure n° | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Durée τ (en s) | 2,08 | 2,05 | 2,06 | 2,13 | 2,08 | 2,07 | 2,09 | 2,05 | 2,08 | 2,09 |
Dans les conditions de l’expérience :
- L’écart-type sur la durée est σn-1 = 2,35·10–2 s
- L’incertitude sur la durée se calcule avec la formule \(\displaystyle\mathrm { U(τ)= \frac{2.26 \ σ_{n-1}}{\sqrt{n}} }\) où n est le nombre de mesures réalisées.
- L’incertitude relative sur la valeur de la vitesse est \(\displaystyle\mathrm { \frac{U(v)}{v} = \sqrt{ \left( \frac{U(τ)}{τ} \right)^2 + \left( \frac{U(d)}{d} \right)^2 } }\)
Expérience n°2
Avec les mêmes réglages, Karim détermine la valeur de la vitesse v de déplacement du chariot à l’aide de l’effet Doppler. Disposant d’une interface d’acquisition et d’un logiciel de traitement, il mesure la fréquence reçue par le récepteur dans deux situations expérimentales :
- Lorsque le chariot est immobile, f1 = 42170 Hz.
- Lorsque le chariot est mouvement, f2 = 42134 Hz.
Dans les conditions de l’expérience :
- Lors de la réflexion sur un obstacle en mouvement, la fréquence de l’onde reçue après réflexion est différente de celle de l’onde émise de fréquence fém.
- La valeur absolue de la variation de fréquence I∆fI est donnée par : \(\displaystyle\mathrm { |∆f|= \frac{2 \ v \ f_{ém}}{c} }\)
- Dans cette relation :
- v est la valeur de la vitesse de déplacement de l’obstacle par rapport à la source ;
- c est la célérité de l’onde.
3.1. Citer une différence entre les ondes utilisées par un LiDAR et celles utilisée dans ces deux expériences.
3.2. Dans le cas de l’expérience n°1, déterminer la valeur de la vitesse de déplacement du chariot, notée vexp1 et exprimer le résultat en prenant en compte l’incertitude associée.
3.3. Lors de l’expérience n°2, le chariot se rapproche-t-il ou s’éloigne-t-il de l’ensemble « émetteur-récepteur ? Justifier.
3.4. L’incertitude relative sur la valeur de la vitesse déterminée dans l’expérience 2 est de 5 %. Les deux expériences donnent-elles des valeurs de vitesses compatibles ?
|







