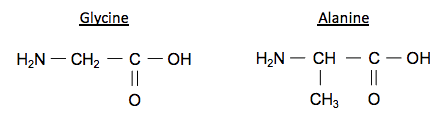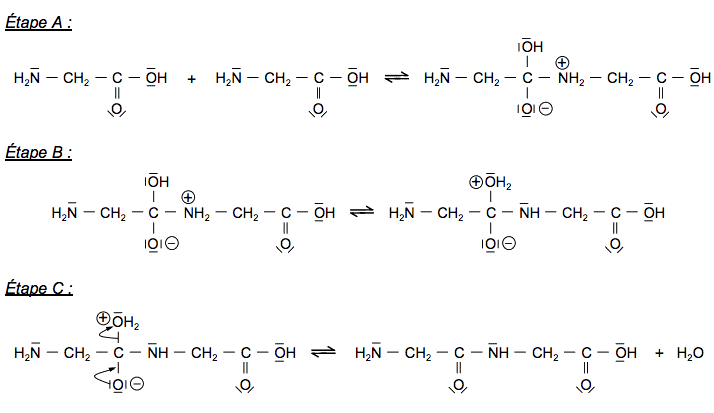Carnet de bac

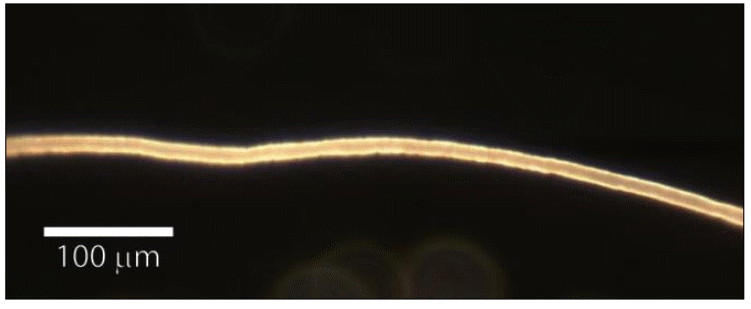
La soie que produisent les araignées pour tisser leurs toiles ou envelopper leurs proies possèdent des propriétés physico-chimiques si exceptionnelles (finesse, régularité, élasticité, solidité, imputrescibilité, etc…) qu’elle est devenue un sujet d’étude pour de nombreux scientifiques.

Cet exercice aborde plusieurs aspects de la soie d’araignée considérée comme un matériau d’avenir.

1. Composition de la soie d’araignée

La soie d’araignée est essentiellement composée de fibroïne, une molécule constituée de plusieurs centaines d’acides aminés reliés les uns aux autres par des liaisons peptidiques. Les deux principaux acides aminés présents dans la fibroïne sont la glycine (40 % environ) et l'alanine (25-30 % environ) dont les formules semi-développées sont indiquées ci-dessous.

Selon l’enchaînement des différents acides aminés au sein de la macromolécule de fibroïne, cette protéine peut adopter deux structures géométriques tridimensionnelles différentes : soit une structure semi-cristalline en feuillets bien ordonnés, soit une structure amorphe inorganisée.

La soie d’araignée est donc un matériau dont les propriétés mécaniques découlent de l’organisation structurale particulière de la molécule de fibroïne : des régions cristallines expliquent la résistance élevée de la soie d’araignée tandis que des régions amorphes sont responsables de son importante élasticité.

1.1. Pourquoi les molécules de glycine et d’alanine appartiennent-elles à la famille des acides aminés ?

1.2. La molécule de glycine possède-t-elle des stéréoisomères ? Argumenter.

1.3. La molécule d’alanine compte deux stéréoisomères. Donner la représentation de Cram de ces deux stéréoisomères, puis justifier le type de relation de stéréoisomérie qui les lie.

1.4. Après avoir hydrolysé les protéines de la soie d’araignée, on en extrait la glycine et l’alanine. On réalise ensuite une spectroscopie RMN du proton afin de caractériser leur présence. Indiquer le nombre de protons équivalents dans chaque molécule et prévoir, en expliquant votre démarche, le nombre et la multiplicité des signaux observés dans chacun des spectres RMN de la glycine et de l’alanine, sachant que les atomes d’hydrogène reliés aux atomes d’oxygène et d’azote n’interviennent pas dans la multiplicité des signaux des atomes d’hydrogène voisins

2. Biomimétisme chimique

Actuellement, les chimistes cherchent à réaliser des fibres artificielles reproduisant les propriétés de la soie d’araignée en créant des polypeptides dont la composition et la structure sont les plus proches possible de celles de la fibroïne. Les polypeptides sont de longues molécules obtenues par l’assemblage de plusieurs acides aminés La réaction permettant d’assembler deux acides aminés est appelée « synthèse peptidique ».

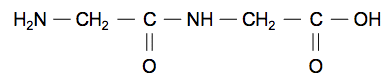
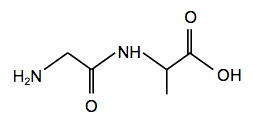
Deux molécules de glycine (Gly), mises en présence, réagissent l’une avec l’autre pour former un dipeptide, usuellement nommé Gly-Gly, dont la formule semi-développée s’écrit :

Le mécanisme réactionnel de la synthèse de ce dipeptide est le suivant :

Pour synthétiser un dipeptide donné, les chimistes protègent au préalable les fonctions organiques qui ne doivent pas réagir ensemble, puis font réagir les fonctions non protégées (synthèse peptidique), et enfin déprotègent les fonctions n’ayant pas participé à la synthèse En l’absence de ces précautions, plusieurs dipeptides différents peuvent être obtenus au terme de la synthèse peptidique.

Donnée : Comparaison des électronégativités de quelques éléments : χ(H) ≈ χ(C) et χ(C) < χ(O)

2.1. Nommer la nouvelle fonction chimique présente dans le dipeptide Gly-Gly.

2.2. Analyse du mécanisme réactionnel

2.2.1. Recopier l'étape A du mécanisme réactionnel de cette synthèse et la compléter par le tracé des flèches courbes nécessaires Justifier précisément l’orientation de la flèche conduisant à la formation de la liaison.

2.2.2. L’étape B de ce mécanisme réactionnel correspond à une « réaction acido-basique intramoléculaire ». Justifier cette appellation.

2.2.3. À quelle catégorie de réaction appartient l’étape C de ce mécanisme réactionnel ? Justifier.

2.3. Combien de dipeptides différents peut-on, a priori, obtenir par synthèse peptidique d’un mélange de glycine (Gly) et d’alanine (Ala), sous la forme d’un unique énantiomère chacun ? Argumenter votre réponse.

2.4. La fabrication de fibres artificielles aussi élastiques et solides que la soie d’araignée utilise le dipeptide Gly-Ala comme motif de base de la chaine polypeptidique. La formule topologique de ce dipeptide est la suivante :

Ce dipeptide étant obtenu par synthèse peptidique en faisant réagir de la glycine (Gly) et de l’alanine (Ala), préciser la (ou les) fonction(s) que l’on doit protéger sur chacune de ces deux molécules pour obtenir uniquement le dipeptide Gly-Ala.

3. Détermination du diamètre d’un fil d’araignée

Un fil d’araignée, de diamètre inconnu noté a, est maintenu en position verticale et éclairé au moyen d’une source laser rouge de longueur d'onde λ = 615 nm. Le fil est placé à quelques centimètres de la source laser et à une distance D assez éloignée d’un écran vertical La figure de diffraction obtenue à l’écran est caractérisée par une tache centrale de largeur L et un angle de diffraction noté θ.

Schéma de l’expérience en vue de profil

Schéma de l’expérience en vue de dessus, sans souci d’échelle

3.1. Quel caractère de la lumière est mis en évidence par l’apparition d’une figure de diffraction ?

3.2. Rappeler l’expression qui lie les grandeurs a, θ et λ Sachant que tan θ = θ pour les faibles valeurs de θ en radian, démontrer que la largeur L de la tache centrale de diffraction admet pour expression littérale : $$\mathrm{ L= \frac{2 \ λ \ D}{a} } $$ 3.3. Calculer, en m puis en µm, le diamètre a du fil d’araignée analysé sachant que D = 2,00 ± 0,01 m et L = 18,8 ± 0,4 cm.

3.4. La source lumineuse étant un laser, on fera l’hypothèse que l’incertitude sur la longueur d’onde peut être négligée par rapport aux autres incertitudes L’incertitude absolue U(a) associée à la mesure du diamètre a du fil d’araignée dépend uniquement des incertitudes absolues U(D) et U(L) associées aux distances D et L selon la relation suivante : $$\mathrm{ \left( \frac{U(a)}{a} \right)^2 = \left( \frac{U(D)}{D} \right)^2+ \left( \frac{U(L)}{L} \right)^2 } $$ Exprimer le résultat de la mesure expérimentale du diamètre a du fil d’araignée sous la forme d’un encadrement.

3.5. Le même fil d’araignée que celui étudié dans la partie précédente est maintenant observé et photographié à l’aide d’un microscope optique équipé d’un appareil photo numérique. Voici le cliché obtenu :

Déterminer le diamètre a du fil à partir du cliché ci-dessus et donner le résultat assorti de l’incertitude absolue U(a) associée à cette valeur. Dans cette mesure, on considère que : \(\displaystyle\mathrm{ \frac{U(a)}{a}=\frac{U(d)}{d} } \) avec d la valeur mesurée sur la photographie et U(d) l’incertitude absolue associée.

3.6. La mesure par diffraction du diamètre du fil d’araignée réalisée dans la partie précédente estelle cohérente avec la mesure effectuée au microscope optique ? Détailler la réponse.

3.7. Quelle méthode est-il préférable d’utiliser pour réaliser cette mesure ? Justifier votre réponse.

4. Élasticité et solidité d’un fil d’araignée

Dans les forêts tropicales d’Amérique, la néphile clavipes est l’une des araignées les plus communes et les plus impressionnantes. Sa toile dépasse souvent un mètre de diamètre, les fils de soie ont des reflets dorés et collent fortement. Si par mégarde, vous prenez une telle toile dans le visage lors d’une sortie nocturne, vous verrez que les fils ne cèdent pas ! Ils sont si résistants que l’on cherche à les utiliser dans la fabrication de gilets pare-balles.

D’après Futura science

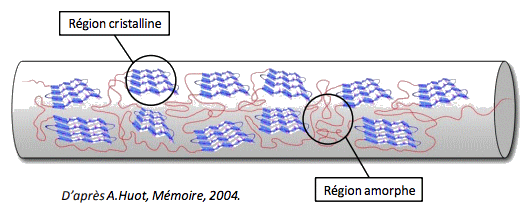
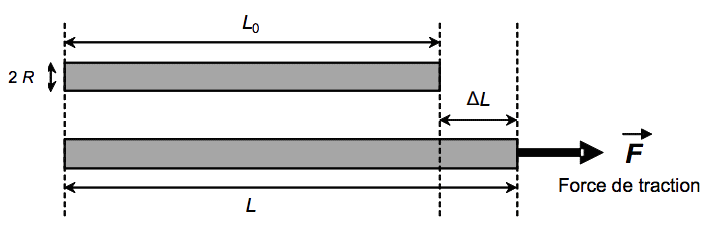
Lorsque l’on soumet une fibre élastique cylindrique de rayon R et de longueur L₀ à une force longitudinale de valeur F appelée « force de traction », la fibre s’allonge et acquiert une nouvelle longueur L > L₀. Aux faibles valeurs de F, l’allongement ΔL = L - L₀ de la fibre est proportionnel à la valeur de la force appliquée et satisfait à la relation suivante : $$\mathrm{ ΔL= \frac{F \ L_0}{E \ π \ R^2} } $$ où E est une constante appelée « module de traction » qui dépend de la nature de la fibre.

Donnée : Intensité de la pesanteur terrestre : g = 9,8 N·kg^-1

4.1. Par une analyse dimensionnelle, vérifier que le module de traction d’une fibre élastique s’exprime en N·m^-2.

4.2. On soumet un fil de soie d’araignée néphile clavipes de rayon R = 2,5 µm et de longueur initiale L₀ = 6,5 cm à une force de traction de valeur F = 0,03 N Le fil s’allonge alors jusqu’à atteindre une longueur L = 7,7 cm. Vérifier que ces valeurs expérimentales sont en accord avec la valeur du module de traction de la soie de cette araignée fournie dans l’énoncé.

4.3. Expliquer qualitativement comment varie l’élasticité d’une fibre en fonction de la valeur de son module de traction, puis comparer les propriétés élastiques d’un fil d’araignée néphile clavipes, d’un cheveu, du nylon et de la laine.

4.4. Sachant qu’un fil de soie de néphile clavipes de rayon R = 2,5 µm peut s’allonger au maximum de 35 % avant de rompre, calculer la masse maximale que l’on peut suspendre verticalement à un tel fil avant sa rupture.