Carnet de bac

Source : FIVB 2012

Au volley-ball, le service smashé est le type de service pratiqué le plus fréquemment par les professionnels : le serveur doit se placer un peu après la limite du terrain, lancer très haut son ballon, effectuer une petite course d'élan puis sauter pour frapper la balle.

D’après Volley-ball

Après la course d’élan, le serveur saute de façon à frapper le ballon en un point B₀ situé à la hauteur h au-dessus de la ligne de fond de terrain. La hauteur h désigne alors l’altitude initiale du centre du ballon. Le vecteur vitesse initiale \(\displaystyle\mathrm{ \vec{v}_0 } \) du ballon est horizontal et perpendiculaire à la ligne de fond du terrain (voir figure 1.). Le mouvement du ballon est étudié dans le référentiel terrestre supposé galiléen muni du repère (Ox, Oy) et l’instant de la frappe est choisi comme origine des temps : t = 0 s. Le mouvement a lieu dans le plan (Oxy).

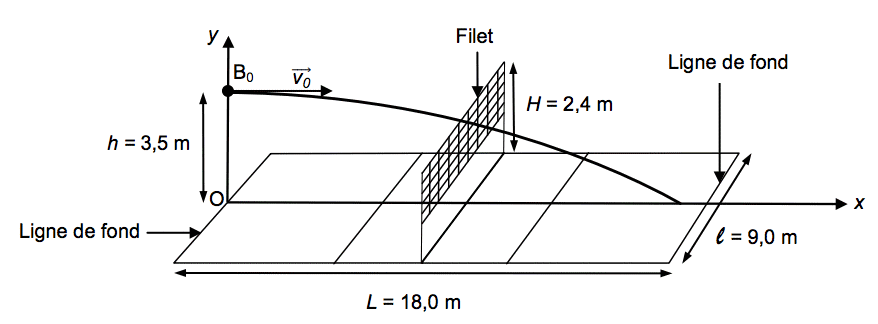
Figure 1. Dimensions du terrain de volley-ball et allure de la trajectoire du ballon.

Le but de cet exercice est de déterminer la valeur de la vitesse initiale du ballon, de vérifier la validité du service et d’étudier la réception du service par un joueur de l’équipe adverse. Pour cela, on étudie le mouvement du centre du ballon sans tenir compte de l’action de l’air, de la rotation du ballon sur lui-même et de ses déformations.

Données :

• le ballon de volley-ball a une masse m = 260 g et un rayon r = 10 cm ;
• intensité du champ de pesanteur : g = 9,81 m·s^-2 ;
• la valeur de la célérité c de la lumière dans le vide ou dans l’air est supposée connue du candidat ;
• domaines des ondes électromagnétiques en fonction de la longueur d’onde λ :
  

1. Mesure de la vitesse initiale du ballon

Figure 2. Radar portatif utilisé
lors de la mesure de la vitesse
(indiquée en km·h^-1).

Afin d’évaluer les performances du serveur, on mesure la valeur de la vitesse initiale v₀ du ballon grâce à un radar portatif (voir figure 2.), que l’on pointe en direction de la position de frappe B₀. Le manuel du radar portatif indique que celui-ci envoie des ondes électromagnétiques haute fréquence (3,47·10¹⁰ Hz) et mesure la différence de fréquence entre l’onde émise et l’onde réfléchie sur un objet en mouvement.

1.1. Identifier le domaine des ondes électromagnétiques émises par ce radar portatif. Justifier par un calcul.

1.2. Nommer le phénomène à l’origine de la différence de fréquence entre les ondes émise et reçue par le radar portatif.

1.3. Le radar portatif est positionné face au serveur et vise le ballon. La fréquence de l’onde reçue est-elle inférieure ou supérieure à celle de l’onde émise ? Justifier.

1.4. Dans les mêmes conditions de mesure que pour la question 1.3, le décalage Δf entre la fréquence fémise de l’onde émise et la fréquence freçue de l’onde reçue vérifie la relation : \(\displaystyle\mathrm{ |Δf|=|f_{reçue} - f_{émise} |= \frac{2 \ v_0 \ f_{émise}}{c} } \) Le décalage |Δf| mesuré par le radar portatif est de 4,86 kHz. En déduire la valeur de la vitesse du ballon. Vérifier l’accord avec l’indication de l’écran du radar portatif de la figure 2.

2. Validité du service

Le service est effectué depuis le point B₀ à la vitesse v₀ = 21,0 m·s^-1. Le service sera considéré comme valide à condition que le ballon franchisse le filet sans le toucher et qu’il retombe dans le terrain adverse.

2.1. Montrer que, si on néglige l’action de l’air, les coordonnées du vecteur accélération du centre du ballon après la frappe sont : a_x(t) = 0 et a_y(t) = −g

2.2. Établir que les équations horaires du mouvement du centre du ballon s’écrivent : \(\displaystyle\mathrm{ x(t) = v_0 \ t } \) et \(\displaystyle\mathrm{ y(t) = - \frac{g \ t^2}{2} + h } \)
En déduire que l’équation de la trajectoire reliant x et y s’écrit : \(\displaystyle\mathrm{ y(x) = - \frac{g \ t^2}{2} + h } \)

2.3. En admettant que le ballon franchisse le filet, vérifier qu’il touche le sol avant la ligne de fond.

2.4. Afin de déterminer la vitesse du ballon au moment où il touche le sol, on effectue une étude énergétique. L’origine de l’énergie potentielle de pesanteur est choisie de la manière suivante : E_pp = 0 J pour y = 0 m.

2.4.1. Rappeler les expressions littérales des énergies cinétique E_c, potentielle de pesanteur E_pp et mécanique E_m du ballon en un point quelconque de la trajectoire.

2.4.2. Le graphe de la figure 3 représente l’évolution en fonction du temps des trois énergies précédentes. Associer chaque courbe 1, 2, 3 à l’une des trois énergies E_m, E_pp, E_c. Justifier.

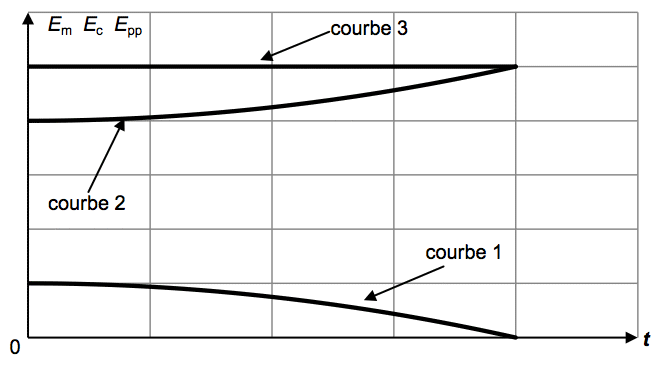
Figure 1. Dimensions du terrain de volley-ball et allure de la trajectoire du ballon.

2.4.3. À l’aide de l’étude énergétique précédente, déterminer la valeur de la vitesse du centre du ballon vsol lorsque le ballon touche le sol.

2.5. En réalité, la vitesse vsol avec laquelle le ballon atteint le sol est plus faible que celle déterminée à la question 2.4.3. Proposer une explication.

3. Réception du ballon par un joueur de l’équipe adverse

Au moment où le serveur frappe le ballon (t = 0 s), un joueur de l’équipe adverse est placé au niveau de la ligne de fond de son terrain. Il débute sa course vers l’avant pour réceptionner le ballon en réalisant une « manchette » comme le montre la figure 4. Le contact entre le ballon et le joueur se fait au point R situé à une hauteur de 80 cm au-dessus du sol.

D’après Le sport dauphinois

On admet que les équations horaires du mouvement du ballon établies à la question 2.2. restent valables. Évaluer la vitesse moyenne minimale du déplacement de ce joueur pour qu’il réalise la réception dans la position photographiée ci-dessus. Ce résultat semble-t-il réaliste ?
Le candidat est invité à prendre des initiatives et à présenter la démarche suivie même si elle n’a pas abouti. La démarche suivie est évaluée et nécessite donc d’être correctement présentée.