Carnet de bac

Les deux parties A et B sont indépendantes.

Partie A. L’éclipse du 21 août 2017

Les Américains l'ont baptisée "The Great American Eclipse" (la grande éclipse américaine). Le 21 août 2017, l'ombre de la Lune traversa les États-Unis du Pacifique jusqu'en Atlantique. Outre-Atlantique, l'événement a soulevé pendant plusieurs mois un enthousiasme extraordinaire.

D’après Science & Avenir

• Constante de gravitation universelle : G = 6,67·10^–11 m³·kg^–1·s^–2
• Masse de la Lune : M_L = 7,34·10²² kg
• Masse de la Terre : M_T = 5,97·10²⁴ kg
• Diamètre de la Lune supposée sphérique : D_L = 3 474 km
• Diamètre de la Terre supposée sphérique : D_T = 12 742 km
• Distance moyenne du centre de la Lune au centre de la Terre : d = 3,84·10⁵ km
• Latitudes et longitudes de quelques villes américaines

	Salem	Columbia	Charleston
Latitude	44,94° Nord	38,94° Nord	32,78° Nord
Longitude	123,04° Ouest	92,33° Ouest	79,93° Ouest

Dans le référentiel géocentrique, la Terre accomplit un tour sur elle-même en environ 23 heures et 56 minutes (durée du jour sidéral). On se place dans ce référentiel pour répondre aux questions ci-dessous.

1.1. Quelle est la nature du mouvement d’un point situé sur l’équateur ?

1.2. Montrer que la valeur de la vitesse d’un point situé sur l'équateur est égale à 465 m·s^-1. La vitesse V, en m·s^-1, d’un point de la surface de la Terre dépend de sa latitude α selon la relation :

V = 465 cos α

1.3. Quelle est la vitesse d’un point de la ville de Columbia ?

2. Vitesse de l’ombre de la Lune sur la Terre

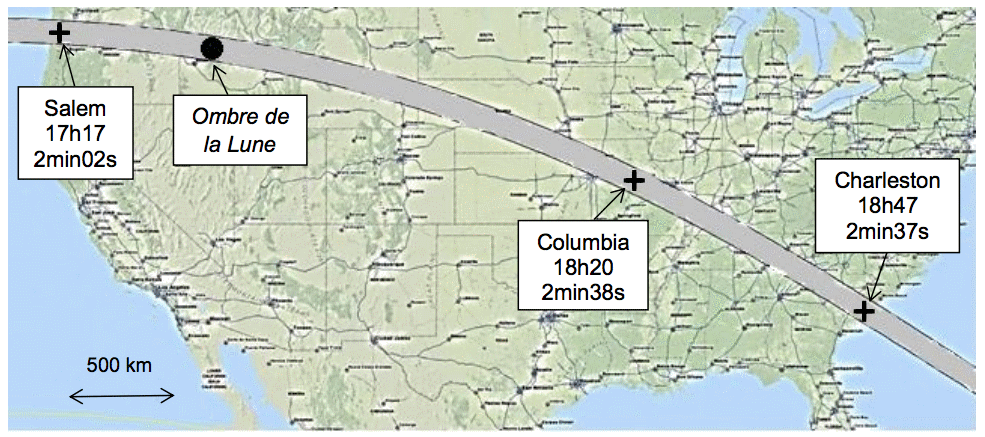
Trajectoire, heures de passage (temps universel), et durée maximale de l’éclipse.

D‘après Wolfgang Strickling —https://commons.wikimedia.org

2.1. En exploitant ce document, montrer que dans le référentiel terrestre la vitesse moyenne V_O de l’ombre de la Lune sur la Terre vaut environ 750 m·s^-1.

2.2. Compte tenu de la durée maximale de l’éclipse en un lieu de son passage, estimer le diamètre de l’ombre de la Lune sur la Terre lors de l’éclipse. Cette valeur est-elle pertinente au regard de la carte ci-dessus ?

3. Mouvement de la Lune autour de la Terre

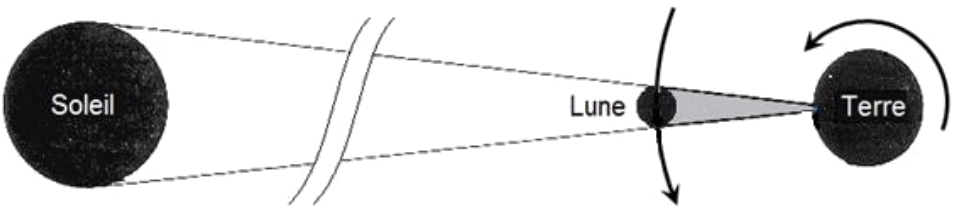
Schéma simplifié des positions de la Terre et de la Lune lors d’une éclipse.

3.1. Pourquoi ne tient-on pas compte du phénomène de diffraction des rayons lumineux par la Lune ? L'argumentation s'appuiera sur des valeurs numériques.

On se place maintenant dans le référentiel géocentrique, supposé galiléen. On étudie le système {Lune}, sans tenir compte de l’influence du Soleil.

3.2. Faire un schéma sur lequel apparaîtront la Terre ainsi que la Lune et son orbite, supposée circulaire. Représenter le vecteur \(\displaystyle\mathrm{ \vec{F}_{T/L}} \) représentant la force modélisant l’interaction gravitationnelle exercée par la Terre sur la Lune, ainsi que le vecteur unitaire \(\displaystyle\mathrm{ \vec{u}} \), orienté depuis la Lune vers la Terre.

3.3. Donner l’expression vectorielle de \(\displaystyle\mathrm{ \vec{F}_{T/L}} \) .

3.4. Établir l’expression vectorielle de l’accélération de la Lune, en fonction de G, MT, d et du vecteur unitaire \(\displaystyle\mathrm{ \vec{u}} \) .

3.5. Montrer que la vitesse de la Lune sur son orbite s’exprime par la relation : \(\displaystyle\mathrm{ V_L=\sqrt{\frac{G \ M_T}{d}} } \)

3.6. Calculer la valeur de cette vitesse.

Partie B. Étude de la couronne solaire

Les éclipses de Soleil ont joué un rôle important en astronomie car elles permettent d'étudier la couronne solaire. C’est au cours de l’une d’elles que l’hélium a été découvert.

Données :

• Célérité de la lumière dans le vide : c = 2,998·10⁸ m·s^-1
• Constante de Planck : h = 6,626·10^-34 J·s
• 1 eV = 1,602·10^-19 J
• Spectre de la couronne solaire :
  

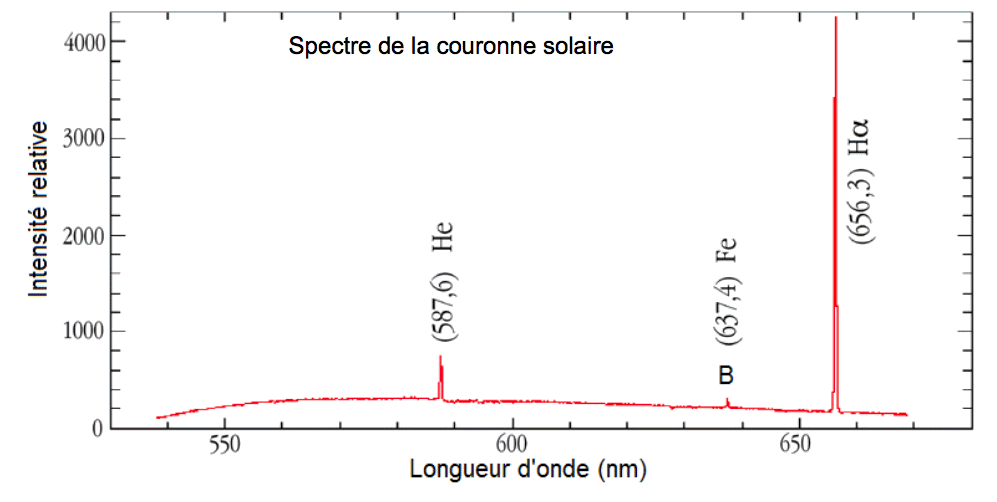
1. Découverte de l’hélium

Le 18 août 1868 l’astronome français Jules Janssen, en observant une éclipse totale de soleil, découvre par spectroscopie un gaz jusque-là inconnu dans l'atmosphère de cet astre. Il sera appelé hélium par référence au mot grec hélios (soleil).

1.1. Le spectre donné de la couronne solaire est-il un spectre d’émission ou d’absorption ? Justifier la réponse.

1.2. À quel domaine du spectre électromagnétique ce spectre appartient-il ? Justifier la réponse.

Extrait du diagramme énergétique de l'atome d’hélium

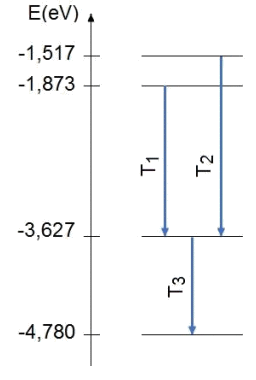
1.3. La radiation émise par l’hélium, observée dans le spectre de la couronne solaire, a permis son identification. À quelle transition T₁, T₂ ou T₃ correspond-elle ?

1.4. Historiquement, cette radiation a été confondue avec celles émises par le sodium de longueur d’onde : 589,0 nm et 589,6 nm. L’utilisation d’un spectromètre dont l’incertitude relative est \(\displaystyle\mathrm{ \frac{U(λ)}{λ}=10^{-3} } \) permet-elle de discerner la radiation émise par l’hélium de celles émises par le sodium ?

2. Le mystère de la couronne solaire

La couronne solaire est formée par des jets de matière, principalement d’hydrogène et d’hélium, issus de la surface du Soleil.

Couronne solaire photographiée lors de l’éclipse du 3 septembre 2016 par Miloslav Druckmüller.

Les astrophysiciens disposent de plusieurs méthodes pour déterminer la température d’un corps dont la loi de Wien et l'élargissement des raies spectrales.

• Loi de Wien : le maximum d’intensité lumineuse d’un corps noir à la température T (K) est obtenu pour la longueur d’onde λ_max telle que \(\displaystyle\mathrm{ λ_{max}=\frac{2.9 \cdot 10^{-3}}{T} } \) (en m).

• Élargissement des raies spectrales : la largeur des raies d’émission des éléments contenus dans un corps permet d’évaluer sa température T (K). En effet, du fait de l'agitation thermique, la longueur d’onde d'émission change légèrement. On montre qu’à mi-hauteur pour l’élément hydrogène, la largeur d’une raie \(\displaystyle\mathrm{ Δλ } \) est donnée par : \(\displaystyle\mathrm{ Δλ=7,2 \cdot 10^{-7} \ λ_0 \ \sqrt{T} } \)

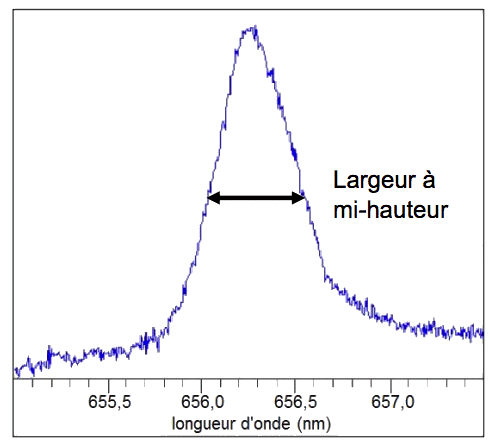
Détail du spectre de la raie H_α de l’hydrogène présent dans la couronne solaire.

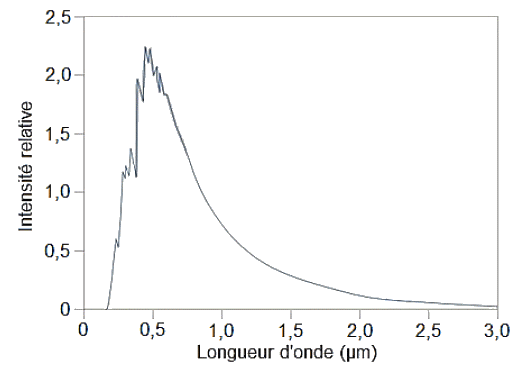
Spectre de la surface du soleil.

2.1. Comparer les températures de la couronne solaire et de la surface du Soleil.

2.2. À quel problème sont confrontés les astrophysiciens dans l'estimation de ces températures ?