La mer, monde du silence ? Poétique, mais faux. L'environnement marin est empli de bruits naturels provenant des vagues, du vent et de la pluie, ainsi que des sons émis par les organismes vivants. Auxquels s'ajoutent, et de manière croissante, les sons d'origine humaine. Une véritable pollution sonore dont les conséquences peuvent être dramatiques pour les mammifères marins, et contre laquelle se mobilise un nombre croissant de scientifiques et d'environnementalistes.
La chlorinité de l’eau de mer peut être considérée comme étant la masse de chlore (exprimée en g) présente dans 1 kg d’eau de mer.
Données :
- Densité de l’eau de mer à 25°C : d = 1,023.
- Masses molaires atomiques : M(Na) = 23,0 g·mol-1; M(Cℓ) = 35,5 g·mol-1.
- La conductivité σ exprimée en S·m-1 d’une solution est donnée par la relation : σ= ∑λi[Xi] où λi est la conductivité molaire ionique exprimée en mS·m²·mol–1 de l’ion Xi et [Xi] sa concentration molaire exprimée en mol·m-3
- Conductivités molaires ioniques à 25°C :
| lon | Na+ | Cℓ– | Ag+ | NO3– |
| λ (en mS·m²·mol–1) | 5,01 | 7,63 | 6,19 | 7,14 |
On prépare 50,0 mL d’eau de mer diluée au dixième. On appelle Smer cette solution. On réalise le titrage conductimétrique de 10,0 mL de la solution Smer par une solution titrante de nitrate d’argent de formule chimique (Ag+(aq) + NO3-(aq)) de concentration molaire c1 = 5,0·10-2 mol·L-1. Lorsqu’on met en présence des ions argent Ag+ et des ions chlorure Cℓ–, il se produit une réaction de précipitation rapide et totale conduisant à la formation de particules solides de chlorure d'argent. L’équation de la réaction modélisant cette transformation chimique s’écrit :
Ag+(aq) + Cℓ–(aq) →AgCℓ(s)
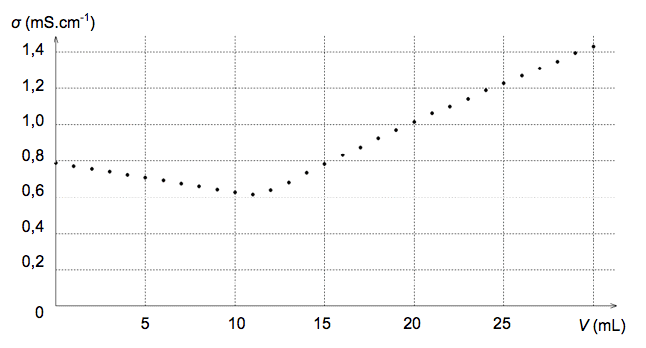
On ajoute à la prise d'essai de 10,0 mL de solution Smer, un volume V = 100 mL d'eau distillée. Après chaque ajout de 1 mL de réactif titrant, on relève la valeur de la conductivité σ, exprimée en mS·cm-1. Le graphe ci-dessous montre l’évolution de la conductivité σ du mélange réactionnel en fonction du volume V de solution de nitrate d’argent versé.
1.1.1. Proposer un protocole de préparation de 50,0mL de solution Smer.
1.1.2. Interpréter qualitativement le changement de pente observé sur le graphe σ = f(V).
1.1.3. Vérifier que la salinité de l’échantillon étudié est voisine de 35 g·kg-1.
1.2. Mesure de la vitesse du son à une profondeur donnée.
Une approximation de la valeur de la vitesse de propagation du son v dans l'eau de mer s'écrit ainsi :
v (en m/s) ≈ 1410 + 4,21 θ – 0,037 θ2 + 1,10 S + 0,018 P
où θ est la température en degrés Celsius, S la salinité en g·kg-1, et P la profondeur en mètres.
Données :
- Vitesse de propagation du son dans l’air ≈ 3·102 m·s-1.
- Évolution de la température θ (en °C) et de la salinité S (en g·kg-1) en fonction de la profondeur.
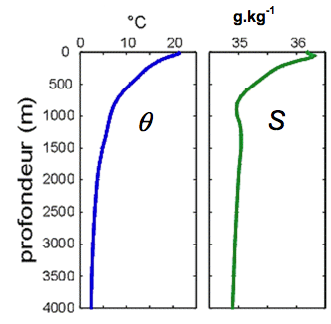
D’après Lecalve
Montrer que l’approximation « Les sons se propagent environ cinq fois plus rapidement dans l’eau que dans l’air » est justifiée lorsqu’on se trouve dans l’eau à une profondeur de 1000 m.
2. Risques auditifs pour les dauphins
Dans la suite de l’exercice, on considère que la valeur de la vitesse du son dans l’eau de mer vaut 1500 m·s-1.
Pour communiquer, les dauphins bleus et blancs produisent des sifflements dont la fréquence peut varier entre 1,1 kHz et plus de 24 kHz et qui peuvent posséder jusqu’à 11 harmoniques.
Données :
- Domaine d’audibilité de l’oreille humaine :
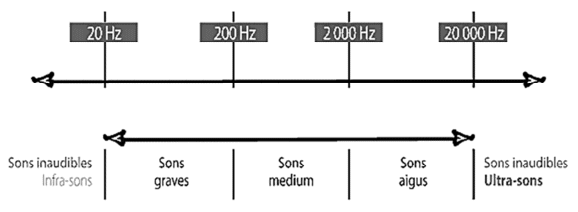
- Seuil d’audibilité à la fréquence 1 kHz pour l’être humain : I0 = 10-12 W·m-2.
D’après l’Ifremer, le seuil de risque auditif pour les cétacés, dont les dauphins, est de 220 dB à 3kHz.
2.1. Signaux émis par les dauphins
2.1.1. Les ondes émises par les dauphins sont des ondes progressives mécaniques : que signifient ces deux derniers termes ?
2.1.2. Les sifflements des dauphins sont-ils audibles par l’homme ? Justifier.
2.1.3. Déterminer la longueur d’onde de l’onde ultrasonore correspondant à un sifflement de fréquence 24,9 kHz émis par un dauphin.
2.1.4. Calculer la valeur de la fréquence des trois premières harmoniques de ce sifflement.
2.2. Impact du son émis par un sonar
Lors d’exercices en mer, certains bateaux militaires utilisent des sonars de forte puissance qui peuvent, par exemple, émettre des signaux d’intensité sonore de 3,2·1011 W·m-2 pour une fréquence égale à 3kHz.
2.2.1. Montrer que le signal du sonar correspond à un niveau d’intensité sonore de 235 dB.
2.2.2. Le son est atténué de 0,16 dB·km-1 dans l’eau de mer.
Estimer la distance minimale à laquelle un dauphin peut se trouver sans subir de risques auditifs. Que penser de ce résultat ?
2.2.3. Lorsque l’émetteur d’une onde de fréquence fE se déplace par rapport au récepteur à une vitesse vE, la fréquence fR de l’onde reçue par le récepteur est différente : le décalage Doppler est donné par la relation \(\displaystyle\mathrm{ f_R=f_E ± \frac{v_E}{v} \ f_E } \) dans le cas où la vitesse de déplacement est faible par rapport à la vitesse de propagation v des ondes.
Le signe est positif dans la relation précédente lorsque l’émetteur s’approche du récepteur et négatif lorsque l’émetteur s’éloigne du récepteur.
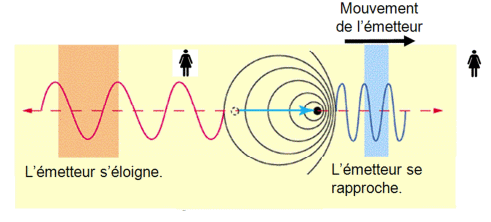
Le sous-marin envoie une onde acoustique de 3kHz en direction du dauphin. Le sous-marin se rapproche du dauphin à la vitesse v égale à 22,0 km·h-1.
a) Le son perçu par le dauphin est-il plus grave ou plus aigu ? Justifier la réponse à partir des données.
b) On considère que le sonar du sous-marin et le dauphin se situent tous les deux à la même profondeur. Calculer la valeur du décalage Doppler. Commenter le résultat obtenu.





