|
L'astronaute Thomas Pesquet s'est envolé dans l'espace pour une mission de longue durée, appelée mission Proxima, lors de laquelle il a mené à bien de multiples activités scientifiques et pédagogiques. Pendant six mois, son domicile et son lieu de travail se sont trouvés à environ 400 kilomètres au-dessus de la Terre.
Thomas Pesquet a décollé à bord d'un lanceur russe Soyouz du cosmodrome de Baikonour au Kazakhstan en novembre 2016, et est revenu sur Terre en mai 2017. Il était accompagné du cosmonaute russe Oleg Novitsky et de l'astronaute de la NASA Peggy Whitson.
D'après un site internet (Proxima - CNES)
L'exercice comporte deux parties A et B indépendantes.
A. À la rencontre de la station spatiale internationale (ISS)
Les systèmes de lanceurs Soyouz mettent des modules habités et des satellites en orbite autour de la Terre depuis près d'un demi-siècle. Ce sont les lanceurs les plus utilisés au monde. Lors du décollage du lanceur Soyouz, quatre propulseurs d'appoint assurent la poussée pendant les deux premières minutes de vol avant d'être largués par le lanceur. Au bout d'environ dix minutes de vol, à une altitude de près de 220 km, le module Soyouz est mis en orbite autour de la Terre, puis après des corrections orbitales, il rejoint l'orbite de la station spatiale internationale à une altitude d'environ 400 km.
Données :
- Rayon de la Terre : RT= 6380 km ;
- Altitude de l'orbite basse du module Soyouz : hs = 220 km ;
- Période orbitale du module Soyouz sur son orbite basse : TS = 88,66 min ;
- Altitude de l'orbite haute du module Soyouz : HS = 320 km ;
- Altitude de la station spatiale internationale (ISS) : hISS= 400 km.
L'étude est conduite dans le référentiel géocentrique ayant pour origine le centre de la Terre et dont les axes pointent vers trois étoiles lointaines. Ce référentiel est supposé galiléen.
1. Orbites du module Soyouz et de l'lSS
Au bout de 10 min de vol, le module Soyouz atteint son orbite basse considérée comme circulaire.
1.1. En utilisant la période orbitale du module Soyouz, déterminer la valeur de sa vitesse VS sur son orbite basse. On considère que le module Soyouz et la station spatiale internationale (lSS) ont des orbites circulaires.
1.2. Démontrer l'expression suivante en explicitant votre démarche : \(\displaystyle\mathrm{ \frac{T_S^2}{(R_T+h_S)^3} = \frac{T_{ISS}^2}{(R_T+h_{ISS})^3} } \)
1.3. Déterminer la valeur de la vitesse VISS de la station spatiale internationale sur son orbite.
2. Orbite de transfert
Pour que le modute Soyouz puisse rejoindre l'orbite de l’lSS des corrections orbitales sont nécessaires. On s'intéresse à présent à une première étape permettant au module Soyouz de se trouver sur une orbite haute plus proche de l'ISS. À un instant donné, lorsque le module Soyouz passe par le point A de son orbite basse, on modifie la valeur de sa vitesse, sans changer sa direction, jusqu'à une valeur V1. Le module Soyouz suit alors une trajectoire elliptique appelée orbite de transfert (figure 1). Lorsque le module Soyouz arrive au point B de son orbite de transfert, il a une vitesse V2. On modifie à nouveau la valeur de sa vitesse, sans changer sa direction, jusqu'à la valeur finale VF qui permet au module de rester sur une orbite haute.
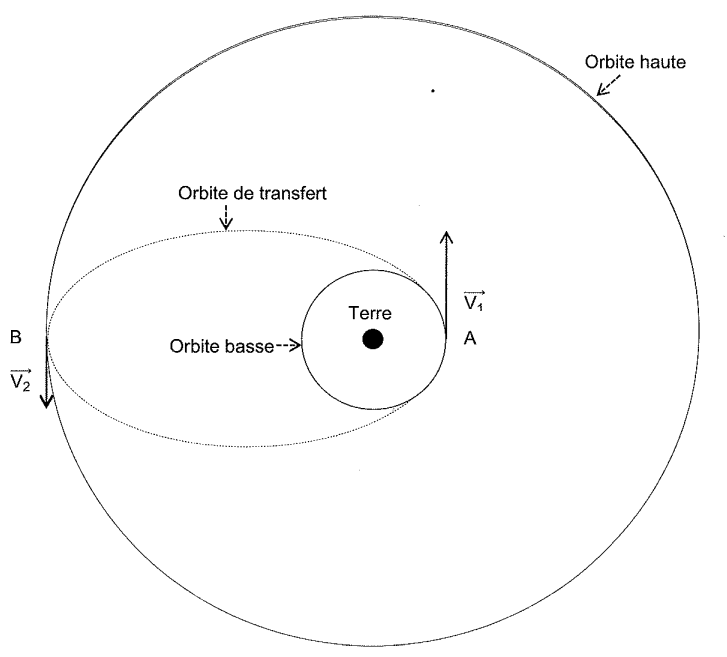
Figure 1 : Représentation de l'orbite de transfert du module Soyouz (sans souci d'échelle)
2.1. Énoncer la deuxième loi de Kepler. En quoi cette loi permet-elle de montrer que V2 < V1 ?
L'expression de l'énergie potentielle Ep du module Soyouz, définie à une constante près, est la suivante :
| \(\displaystyle\mathrm{ E_p=- G\frac{m \ M_T }{R_T+h} } \) |
avec
m : la masse du satellite ;
G = 6,67·10-11 m3·s-2·kg-1 : la constante de gravitation ;
MT = 5,98·1024 kg : la masse de la Terre ;
h : l'altitude du vaisseau Soyouz. |
2.2. Montrer que |’énergie potentielle Ep (B) du module Soyouz au point B est plus grande que l'énergie Ep (A) au point A.
2.3. Justifier que l’énergie mécanique du module Soyouz sur son orbite de transfert entre les points A et B ne varie pas.
2.4. En déduire si la variation d’énergie cinétique entre A et B est positive ou négative. Ce résultat est-il en accord avec la 2ème loi de Kepler ?
2.5. Exprimer l'énergie mécanique du module Soyouz au point A en fonction de m, G, MT, hS, RT et V1.
2.6. Sachant que la valeur de la vitesse V1, est égale à 7,80·103 m·s-1, déterminer la valeur de la vitesse V2. Ce résultat est-il en accord avec les résultats précédents ?
3. Ajustement final
Que faut-il faire ensuite pour que le module Soyouz atteigne la station spatiale ISS ?
B. Échographe télé-opéré
4. Ondes ultrasonores
L’une des expériences mise en œuvre au cours de la mission Proxima, appelée ECHO met en œuvre un échographe télé-opéré depuis la Terre.
L’objectif est d'illustrer le principe du fonctionnement d'un échographe.
Les ondes sonores ou ultrasonores sont des ondes mécaniques longitudinales.
4.1. Préciser la signification du mot longitudinale.
4.2. Citer une différence qui existe entre une onde ultrasonore et une onde sonore.
La mesure de la célérité des ondes ultrasonores dans un milieu donné peut être réalisée en laboratoire. Le principe de l’expérience peut être schématisé comme indiqué ci-dessous (figure 2).
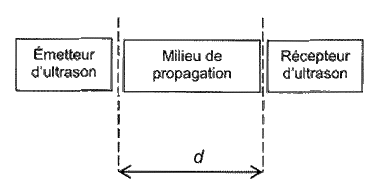
Figure 2 : Principe de l'expérience de mesure de célérité d'une onde
À l'instant t = 0 s, l'émetteur émet une salve ultrasonore. Le signal présenté à ta figure 3 est celui reçu par le récepteur lorsque le milieu de propagation est l’air.
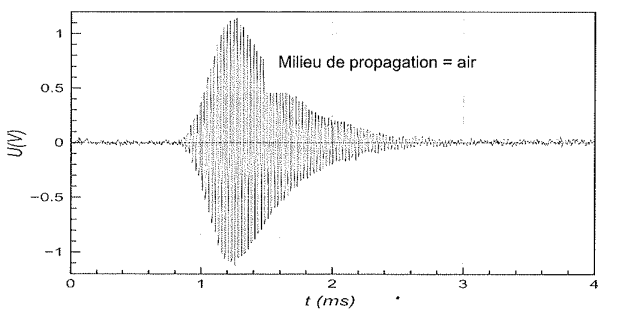
Figure 3 : Signal reçu par le récepteur (1ère expérience)
4.3. Déterminer la valeur du retard entre l'émission et la réception.
4.4. Sachant que la distance d entre l'émetteur et le récepteur vaut 30,0 cm, en déduire la valeur de la célérité des ondes ultrasonores dans ce milieu.
4.5. Commenter le résultat en regard de la nature du milieu de propagation.
5. Principe de l'échographie
Afin de procéder à la télédétection, on piace maintenant l'émetteur et le récepteur côte à côte, face à un écran réfléchissant.
L’origine des dates t=0 s est encore l’instant de l'émission. Pour le signal reçu par le récepteur,on obtient le résultat visible sur la figure 4.
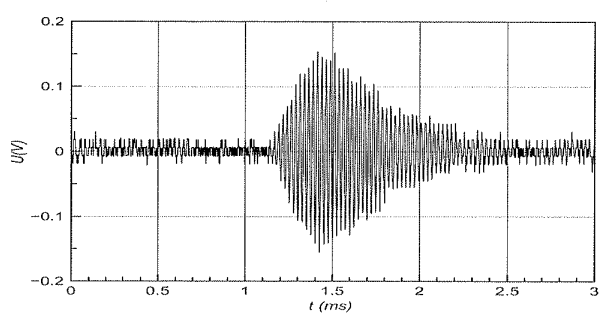
Figure 4 : Signal reçu parle récepteur (2ème expérience)
Déterminer la valeur de la distance émetteur-écran.
6. Application de l'échographie
L'échographie est fondée sur cette méthode de télédétection. La sonde envoie des ultrasons dans le corps du patient qui sont réfléchis à chaque fois qu'ils rencontrent un changement de milieu. Ces échos peuvent alors être reçus par la même sonde. À l'aide d’une échographie, on peut déterminer la taille d'un organe a l'intérieur d'un corps humain. La figure 5 présente le principe de l'échographie.
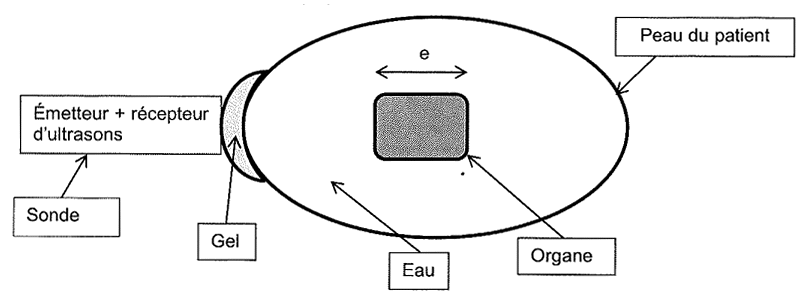
Figure 5 : Principe de l'échographie
L'épaisseur de gel est négligeable.
À l'instant t=0 s, la sonde émet des ultrasons. On visualise deux échos aux instants t1=100 μs et t2=150μs.
6.1. À quoi correspondent les deux échos reçus parla sonde à deux instants différents t1 et t2 ?
6.2. Sachant que la célérité des ondes ultrasonores clans l'organe est égale à 1,54·103 m·s-1, déterminer la valeur de la taille e de l'organe étudié. Commenter le résultat obtenu.
Le candidat est invité à consigner ses pistes de recherche même si celles-ci n'ont pas abouti.
|






