Carnet de bac
Annales
Le kiiking, sport extrême en Estonie |
|
| Polynésie 2018 - Exercice 2 - 7 points |
|
Le kiiking est un sport extrême inventé en 1996 en Estonie. Il s’agit, pour le sportif, de faire un tour complet sur des structures métalliques spécifiques. Debout, ses pieds sont attachés à une planche reliée à des câbles en acier, le tout formant un ensemble rigide. Le sportif de l’extrême fixe la longueur des tiges avec lesquelles il va tenter de faire un tour complet. Le record inscrit dans le livre Guinness, réalisé en 2015 par l’actuel champion de la discipline, correspond à une longueur de tige égale à 7,15 m. D’après Wikipédia.fr
Toute l'étude mécanique est effectuée dans le référentiel terrestre considéré comme galiléen. On considèrera les forces de frottement comme négligeables.
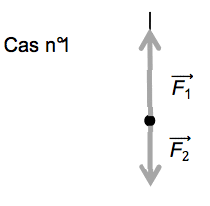
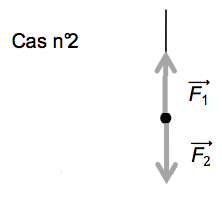
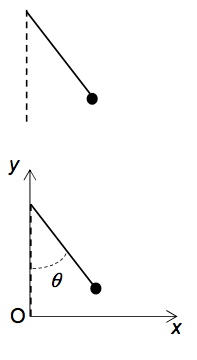
1.2. Recopier le schéma ci-contre représentant le système dans une position quelconque. Représenter les deux forces qui s’exercent sur celui-ci. Que peut-on dire du vecteur vitesse du système lors du mouvement de celui-ci ?
|
| Annexe | |
|
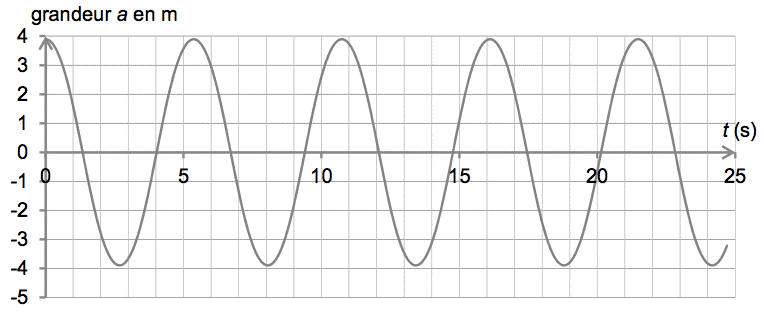
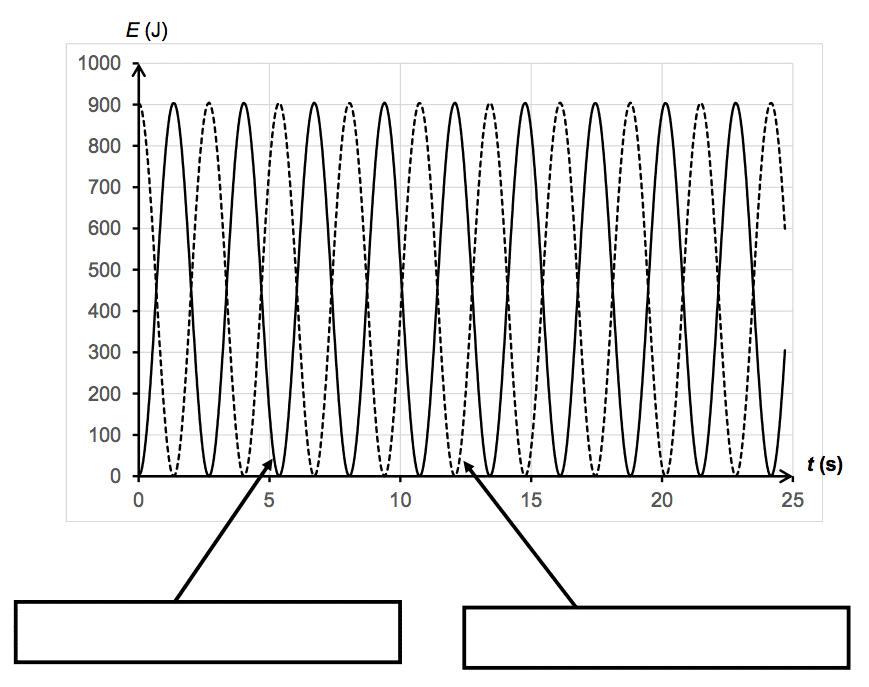
Questions 2.1.et 2.2.
| |