Carnet de bac

Pour se diriger dans l'obscurité ou chasser des insectes, certaines chauves-souris ont développé un système de sonar fondé sur la production et la réception d’ultrasons : l'écholocation.

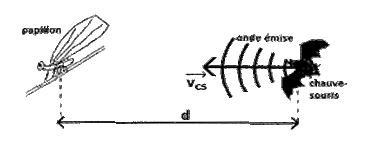
Figure 1. Schéma représentant une situation de chasse par une chauve-souris

Certains papillons « de nuit » sont en mesure d'entendre les émissions sonores des chauves-souris qui cherchent à les repérer. Pour les éviter, ils se laissent alors tomber de la branche sur laquelle ils se trouvent.
Cette tactique semble efficace, car seulement 7 % des papillons qui l'utilisent sont capturés contre 50 % de ceux qui ne l'utilisent pas (Pro Natura, 1999).

D’après Futurascience

L’objectif de l'exercice est d'étudier le principe de l’écholocation et la tactique de défense des papillons de nuit.

Données :

• la fréquence sonore supposée émise par la chauve-souris est : f_e= 50,0 kHz ;

• vecteur vitesse de la chauve-souris : \(\displaystyle\mathrm{ \vec{V}_{CS} } \) ;

• vitesse de l’onde émise par la chauve-souris : v_onde = 340 m·s^-1 ;

• intensité de la pesanteur: g = 9,8 m·s^-2 ;

• masse du papillon : m = 0,50 g ;

• altitude du papillon avant la chute : h = 1,2 m.

1. Étude du sonar de la chauve-souris

1.1. Onde émise par la chauve-souris

1.1.1. À quel domaine de fréquence appartient l’onde émise par la chauve-souris ?

1.1.2. Est-ce une onde mécanique ou électromagnétique ? Justifier.

1.1.3. Cette onde est-elle transversale ou longitudinale ? Justifier.

1.2. Vitesse de la chauve-souris

En utilisant l’effet Doppler, il est possible d’évaluer la vitesse V_cs d'une chauve-souris. Pour une chauve-souris se rapprochant d’un récepteur d’ultrasons, le dispositif mesure une fréquence f_r différente de la fréquence émise par la chauve-souris.

Données :

• fréquence mesurée par le récepteur : f_r = 50,8 kHz
• pour un émetteur en mouvement se rapprochant d'un récepteur fixe, la relation due à l’effet Doppler entre f_a, fréquence émise par la source, et f_r, fréquence reçue par le récepteur, est donnée par : \(\displaystyle\mathrm{ f_r= f_e \ \frac{V_{onde}}{V_{onde}-V_{émetteur}} } \)

1.2.1. Montrer que la valeur de la vitesse de la chauve-souris V_cs est proche de 19 km·h^-1.

1.2.2. Comparer V_onde et V_cs. Expliquer en quoi ce résultat est important pour le déplacement ou la chasse de la chauve-souris.

1.3. Écholocation

La durée mise par les ondes pour revenir à la chauve-souris permet à cette dernière, après réflexion de l’onde sur une proie, d’apprécier la distance la séparant de cette proie, un papillon par exemple.

Le signal émis par la chauve-souris lui revient après une durée \(\displaystyle\mathrm{ τ = 16,7 \ ms} \) . Estimer la distance qui sépare la chauve-souris du papillon.

2. La tactique défensive du papillon

Le but de cette partie est d’étudier cette tactique de défense qui consiste pour le papillon à se laisser tomber. Nous allons déterminer si le papillon peut se protéger, par cette méthode, d'une chauve-souris distante de d = 2,8 m.

On considère que le papillon est immobile au point C (figure 2), avant de se laisser tomber de la feuille. On prendra comme origine des temps, l'instant où le papillon commence à se laisser tomber.

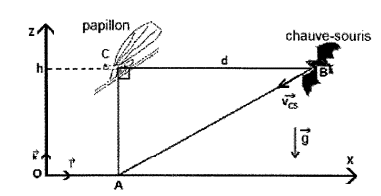
Figure 2. Schéma représentant les positions initiales du, papillon et de la chauve-souris.

2.1. On étudie le mouvement du papillon dans le repère (O ; \(\displaystyle\mathrm{ \vec{i} } \) ; \(\displaystyle\mathrm{ \vec{k} } \) ), en négligeant les forces de frottement de I’air sur le papillon ainsi que la poussée d’Archimède dans I’air. On repère le centre du papillon par un point G comme l'indique la figure 3.

Figure 3 : Schéma représentant la position initiale du papillon.

2.1.1. Établir l'expression du vecteur accélération \(\displaystyle\mathrm{ \vec{a}_G } \) du papillon en appliquant la deuxième loi de Newton au système {papillon} dans le référentiel terrestre supposé galiléen.

2.1.2. Établir l’équation horaire z(t) du mouvement du point G.

2.1.3. En déduire que l’expression de la durée de chute Δt_chute correspondant à l’arrivée du papillon au niveau du sol s'écrit : \(\displaystyle\mathrm{ Δt_{chute}=\sqrt{\frac{2 \ h}{g}} } \).

2.1.4. Vérifier que l'expression \(\displaystyle\mathrm{ \sqrt{\frac{2 \ h}{g}} } \) est bien homogène à un temps.

2.1.5. Calculer la durée nécessaire au papillon pour arriver au niveau du sol (point A) et ainsi être protégé.

2.2. On considère la vitesse de la chauve-souris constante et égale à la valeur V_cs déterminée précédemment. Conclure quant à l'efficacité de la tactique du papillon pour se protéger.

3. Le camouflage optique du papillon

L’iridescence est la propriété de certaines surfaces qui semblent changer de couleur selon l'angle de vue ou d’éclairage. Elle est bien visible sur les ailes de mouches, de libellules et de certains papillons. Ce phénomène provient d'une couche mince recouvrant ces ailes et produisant des couleurs interférentielles. Dans le cas des papillons, les ailes contiennent des écailles de fond et des écailles de recouvrement, disposées à la manière des tuiles d'un toit. La structure de ces écailles et les pigments qu’el|es contiennent jouent un rôle dans la couleur observée. (...)

D’après CNRS.fr

Dans cette partie, le phénomène qui permet à ces papillons de se protéger des prédateurs est modélisé de façon simplifiée. Dans ce modèle élémentaire, schématisé sur la figure 4, on considère que :

• les écailles de l'aile du papillon sont assimilables à des couches minces à faces parallèles d’épaisseur constante e ;

• les ondes issues des chemins (1) et (2) interfèrent au niveau de la rétine de l'observateur ;

• l'aile du papillon est éclairée par de la lumière.

Figure 4. Schéma du trajet d’un rayon lumineux arrivant sur une écaille de l’aile du papillon

Données :

• la vitesse de la lumière dans l’air est notée c et sa valeur est supposée connue.

• épaisseur des couches minces modélisant les écailles de l’aile du papillon : e = 100 nm ;

• indice optique des couches minces principalement composée de chitine : n = 1,5 ; on admet que cet indice ne dépend pas de la longueur d’onde.

• une onde lumineuse monochromatique est caractérisée par une période temporelle T et une longueur d'onde λ ;

• domaines de longueurs d’ondes de la lumière visible :

  Couleur	Violet	Bleu	Vert	Jaune	Orange	Rouge
  Domaine de longueurs d'ondes (nm)	380-446	446-520	520-565	565-590	590-625	625-780

On note \(\displaystyle\mathrm{ τ } \) le retard de l'onde lumineuse qui a suivi le trajet (2) par rapport à l’onde qui a suivi le trajet (1).

3.1. Pour une onde lumineuse monochromatique de période temporelle T, justifier qu’il y a interférences constructives pour \(\displaystyle\mathrm{ τ= k \ T } \) et interférences destructives pour \(\displaystyle\mathrm{ τ=\left( k + \frac{1}{2} \right) \ T } \) où k est un nombre entier.

3.2. Lorsque la lumière blanche arrive perpendiculairement à la surface de l’aile, le retard \(\displaystyle\mathrm{ τ } \) peut s'écrire : \(\displaystyle\mathrm{ τ= \frac{2 \ n \ e }{c}+ \frac{T}{2} } \)

3.2.1. Quelles ondes monochromatiques peuvent conduire à des interférences constructives ?

3.2.2. En déduire la couleur qui sera principalement perçue par l’observateur.

3.3. Lorsque la lumière blanche n’arrive pas perpendiculairement à la surface de l'aile, le retard a pour expression : \(\displaystyle\mathrm{ τ= \frac{2 \ n \ e \ cosθ }{c}+ \frac{T}{2} } \)

Expliquer pourquoi la couleur de l’aile de papillon perçue par l'observateur sera différente s'il la regarde sous un autre angle.