Carnet de bac
Annales
Modélisation d'un parachute au laboratoire |
➔ |
| Amérique du nord 2018 - Exercice 2 - 6 points |
| 1.1) | |||
| D'après la deuxième loi de Newton appliquée au système soumis à son poids, la force d'Archimède et la force de frottement dans un référentiel terrestre supposé galiléen | \(\displaystyle\mathrm{ \vec{P}+ \vec{F}_A+ \vec{f}=m \ \vec{a} } \) | ||
1.2) |
|||
| On sait que | \(\displaystyle\mathrm{ P=m \ g } \) | ||
| D'après l'énoncé | \(\displaystyle\mathrm{ F_A= \frac{4}{3} \ π \ r^3 \ ρ_{air} \ g } \) | ||
| donc | \(\displaystyle\mathrm{ \frac{F_A}{P}= \frac{4 \ π \ r^3 \ ρ_{air} }{3 \ m} } \) | ||
| D'après les données | \(\displaystyle\mathrm{ \frac{F_A}{P}= \frac{4 \times 3,14 \times 0,10^3 \times 1,2}{3 \times 0,400} } \) | ||
| soit | \(\displaystyle\mathrm{ \frac{F_A}{P}= 0,013 } \) | ||
| donc la poussée d'Archimède est négligeable devant le poids. | |||
2.1) |
|||
| D'après la définition de l'énergie cinétique | \(\displaystyle\mathrm{ E_c = \frac{1}{2} \ m \ v^2 } \) | ||
| donc | \(\displaystyle\mathrm{ v= \sqrt{\frac{2 \ E_c}{m}} } \) | ||
| donc la vitesse est proportionnelle à la racine carrée de l'énergie cinétique | |||
| D'après le graphe, on peut distinguer deux phases : durant la première, la vitesse augmente de manière continue alors que pendant la seconde, la vitesse est quasiment constante. Cela peut se justifier en supposant que la première partie est assimiable à une chute libre, alors que pendant la seconde phase, les forces appliquées au système se compensent. | |||
2.2) |
|||
| D'après le graphe on constate que la vitesse limite vaut | \(\displaystyle\mathrm{ v_{lim} = \sqrt{\frac{2 \times 2,5}{0,400}} } \) | ||
| soit | \(\displaystyle\mathrm{ v_{lim} = 3,5 \ m \cdot s^{-1} } \) | ||
2.3) |
|||
| On sait que la variation de l'énergie potentielle de pesanteur s'écrit | \(\displaystyle\mathrm{ ΔEp= m \ g \ Δz } \) | ||
| soit | \(\displaystyle\mathrm{ Δz = \frac{ΔEp}{m \ g} } \) | ||
| D'après les données | \(\displaystyle\mathrm{ Δz= \frac{0-12}{0,400 \times 9,8} } \) | ||
| soit | \(\displaystyle\mathrm{ Δz= - 3,1 \ m } \) | ||
2.4) |
|||
| D'après le graphe, on constate que pendant la première phase du mouvement l'énergie mécanique du système diminue légèrement puis qu'elle diminue régulièrement durant la seconde phase. On en déduit que les forces de frottements sont négligeables pendant la première phase alors qu'elles ne le sont plus pendant la seconde phase du mouvement. | |||
2.5) |
|||
| D'après le graphe, on constate que la variation de l'énergie mécanique pendant la phase du mouvement uniforme vaut | \(\displaystyle\mathrm{ ΔE_m= 2-15=-13 \ J } \) | ||
2.6) |
|||
| On note W le travail de la force de frottement pendant la phase de mouvement uniforme | |||
| On sait que la variation de l'énergie mécanique s'écrit | \(\displaystyle\mathrm{ ΔE_m= W } \) | ||
| On sait que le travail de la force de frottement pendant la phase de mouvement uniforme s'écrit | \(\displaystyle\mathrm{ ΔE_m= f \ Δz } \) | ||
| soit | \(\displaystyle\mathrm{ f = \frac{ΔE_m}{Δz} } \) | ||
| D'après les données | \(\displaystyle\mathrm{ f= \frac{13}{3,1} } \) | ||
| soit | \(\displaystyle\mathrm{ f= 4,2 \ J } \) | ||
3) |
|||
| Si la chute se fait dans le vide alors il s'agit d'une chute libre. Dans ce cas l'énergie mécanique du système est constante au cours du temps. | |||
| On montre que | \(\displaystyle\mathrm{ v(t)=- \ g \ t } \) | ||
| et | \(\displaystyle\mathrm{ z(t)=H - \frac{1}{2} \ g \ t^2 } \) | ||
| donc | \(\displaystyle\mathrm{ E_c= \frac{1}{2} \ m \ g^2 \ t^2 } \) | ||
| et | \(\displaystyle\mathrm{ E_p = m\ g \ \left[ H - \frac{1}{2} \ g \ t^2 \right] } \) | ||
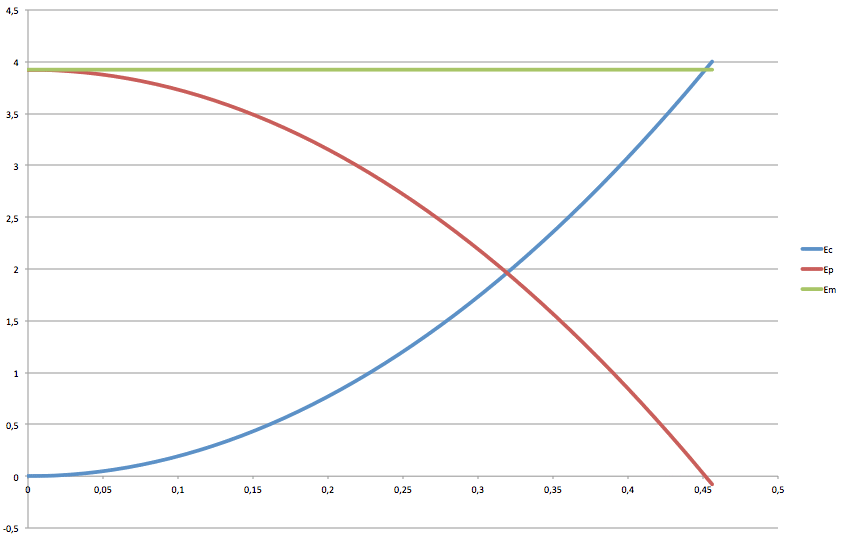
On obtient alors les courbes suivantes où
|
|||
| Carnets de science.xyz |