|
En 1911, le physicien Viktor Hess découvrait ce qui est appelé le rayonnement cosmique. On comprendra par la suite que ce rayonnement est constitué de particules, parmi elles se trouvent des muons.
1. Étude des muons
Lors de son émission de radio « La Conversation scientifique » du 31 décembre 2016 sur France-Culture, Étienne Klein a invité Sébastien Procureur physicien nucléaire, responsable scientifique à l'lRFU (Institut de recherche sur les lois fondamentales de l'univers) du CEA. Au cours de cette conversation, Étienne Klein soulève un point qui pose problème : « En admettant même que ces particules aillent à la vitesse de la lumière, si leur durée de vie est de 2,0 μs, elles parcourent 600 m dans l'atmosphère. Or on a dit qu'elles étaient produites à plusieurs dizaines de kilomètres au-dessus de la surface du sol. Comment on explique ce décalage ? »
La réponse de Sébastien Procureur est limpide : « C'est un simple effet de relativité restreinte. »
Sur le site www.laradioactivite.com. on peut lire : Un muon de 1 GeV (1000 MeV) parcourt en moyenne 6,87 km dans l'atmosphère, un muon de 10 GeV prés de 63 km. Cet allongement des parcours avec l'énergie est dû à la dilatation des durées prédite par la théorie de la relativité restreinte d'Einstein.
Données :
- 1eV =1,60·10-19 J ;
- facteur de Lorentz : \(\displaystyle\mathrm{ γ = \sqrt{\frac{1}{1-\frac{v^2}{c^2}}} }\) où v est la vitesse de la particule dans le référentiel du laboratoire ;
- la durée de vie ΔT d'une particule animée d'une vitesse v, mesurée dans le référentiel du laboratoire, est liée à sa durée de vie propre ΔT0 par l'égalité : ΔT= γ ΔT0 .
- énergie d'une particule de masse m en mouvement : E = γ m c2 ;
- masse du muon : mμ = 1,88·10-28 kg.
1.1. Retrouver l'ordre de grandeur de la valeur de l célérité c de la lumière à partir des valeurs évoquées par Étienne Klein.
1.2. La durée de vie des muons dans leur référentiel propre est ΔT0 = 2,2 μs. Pour des muons qui se déplacent à la vitesse v = 0,9997 c, déterminer la valeur de leur durée de vie mesurée dans le référentiel du laboratoire.
1.3. Quelle est la distance parcourue par ces muons dans le référentiel du laboratoire. Est-elle compatible avec les observations ?
1.4. Quelle est l'énergie d'un muon qui se déplace à la vitesse v = 0,9997 c ? La valeur trouvée est-elle cohérente avec les résultats précédents et les informations fournies ? Justifier.
2. Détection des muons au lycée

Le dispositif ministériel Sciences à l'École, dans le cadre du plan d'équipement COSMOS à l'École, met à disposition des établissements scolaires un cosmodétecteur. Cet appareillage permet de détecter des muons et de mesurer des durées de vie.
Source : Sciences à l'École
Distribution angulaire de la direction d'arrivée des muons
Afin de pouvoir comparer les données de mesures, certains paramètres doivent être réglés sur le cosmodétecteur. Parmi ces paramètres figure l'orientation de l'appareil. Le nombre de muons détectés à la surface de la Terre diffère suivant la direction d'observation.
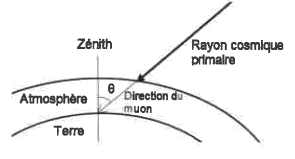
En mesurant le nombre d'impacts en cinq minutes sur le détecteur en fonction de l'angle d'orientation de ce détecteur par rapport au zénith, on trace le graphe suivant :
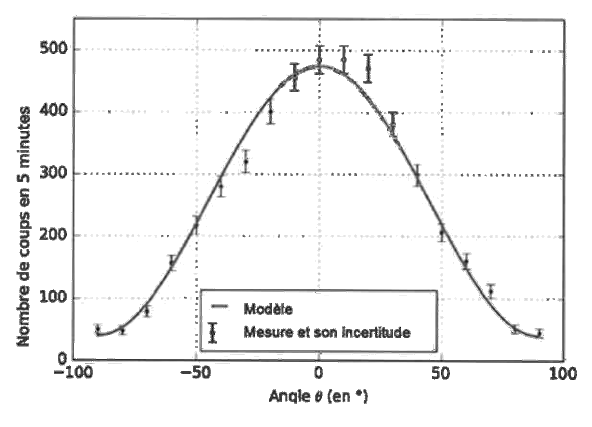
D'après Cahier pédagogique - Plan d'équipement COSMOS à l'École
Mesures collaboratives
À l'occasion de la « Fête de la Science » le vendredi 13 octobre 2017, des mesures ont été effectuées par différents lycées de France. On s'intéresse aux mesures effectuées au lycée de Lunel. Lunel est une ville qui se situe à une altitude de 8 m au-dessus du niveau de la mer (dans le département de l’Hérault). Les mesures ont été effectuées en extérieur de 8 h à 12 h.
Température
(en °C arrondi au dixième) | Pression
(en hPa arrondi au dixième) | Humidité
(%) | Numéro de la mesure | Heure métropole (début de la mesure) | Nombre de muons comptés
au zénith pendant une
durée de 10min |
| 11,4 | 1026,2 | 84 | 0 | 8:00:00 | |
| | | | 1 | 8:00:00 | 1009 |
| | | | 2 | 8:10:00 | 1030 |
| 12 | 1026 | | 3 | 8:20:00 | 992 |
| | | | 4 | 8:30:00 | 994 |
| | | | 5 | 8:40:00 | 1019 |
| 15 | 1026 | 83 | 6 | 8:50:00 | 984 |
| | | | 7 | 9:00:00 | 922 |
| | | | 8 | 9:10:00 | 1008 |
| 15 | 1026 | | 9 | 9:20:00 | 1001 |
| | | | 10 | 9:30:00 | 1016 |
| | | | 11 | 9:40:00 | 971 |
| 16,1 | 1027 | 70 | 12 | 9:50:00 | 940 |
| | | | 13 | 10:10:00 | 963 |
| | | | 14 | 10:20:00 | 990 |
| 18 | 1027 | | 15 | 10:30:00 | 906 |
| | | | 16 | 10:40:00 | 936 |
| | | | 17 | 10:50:00 | 944 |
| 18,1 | 1027,6 | 68 | 18 | 11:00:00 | 927 |
| | | | 19 | 11:10:00 | 919 |
| | | | 20 | 11:20:00 | 965 |
| 18 | 1027 | | 21 | 11:30:00 | 918 |
| | | | 22 | 11:40:00 | 912 |
| | | | 23 | 11:50:00 | 976 |
| 17 | 1027 | 76 | 24 | 12:00:00 | 950 |
Données :
- Le flux de muons au niveau de la mer est de 1 muon par cm2 par minute ;
- Exploitation d'une série de mesures d'une grandeur X :
Pour une série de mesures pour lesquelles on suppose les conditions de répétabilité vérifiée, on considère que la meilleure estimation de l'incertitude de mesure de la grandeur X, avec un niveau de confiancede 95%.
| \(\displaystyle\mathrm{ U_X= 2 \frac{s_{n-1}}{\sqrt{n}} }\) | n : nombre de valeurs disponibles
sn-1 : écart-type expérimental tel que \(\displaystyle\mathrm{ s_{n-1}=\sqrt{\frac{\sum_{i=1}^n(x_i-\bar{x})^2}{n-1}} }\) |
2.1. Dans quelle direction faut-il orienter le détecteur pour avoir un nombre d'impacts maximal ? Ce positionnement doit-il être effectué avec précision ?
2.2. On souhaite évaluer le nombre d'impacts à Lunel en 10 minutes en faisant apparaître la valeur de l'incertitude avec un niveau de confiance de 95 %.
2.2.1. Quelle est la meilleure estimation de ce nombre d'impacts ? Calculer ce nombre.
2.2.2. Écrire le résultat en faisant apparaître la valeur de l'incertitude sur la mesure.
2.3. Évaluer la surface effective de détection du cosmodétecteur. Commenter le résultat.
|




