|
Le badminton est un sport de raquette qui réunit deux joueurs ou deux binômes de joueurs, placés dans deux demi-terrains séparés par un filet. Les joueurs marquent des points en frappant un volant à l'aide d'une raquette pour le faire tomber dans le terrain adverse.
Le volant, d'une masse m égale à 5.0 g, est un projectile aux propriétés aérodynamiques particulières qui lui donnent une trajectoire très différente des balles utilisées dans la plupart des sports de raquette. En effet, les plumes créent une traînée, modélisée par une force \(\displaystyle\mathrm{ \vec{F} } \) , qui s'oppose au mouvement du volant dans l'air.
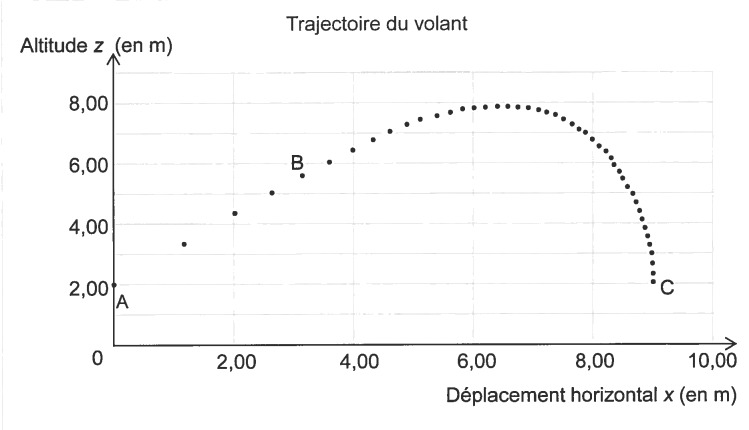
Le mouvement du volant de badminton est étudié dans le référentiel terrestre supposé galiléen auquel est associé le repère d'espace (Ox, Oz). L'exploitation de la vidéo du mouvement du volant permet d'obtenir le graphe reproduit sur I’annexe à rendre avec la copie. L'intervalle de temps entre deux points de mesure vaut Δt = 50 ms.
1. Première approche
1.1. Justifier le fait que le volant n'est pas en chute libre.
1.2. Comment peut-on en première approximation décrire le mouvement du volant sur la portion AB de sa trajectoire ? Représenter sur le graphe reproduit sur I’annexe à rendre avec la copie, le vecteur accélération \(\displaystyle\mathrm{ \vec{a} } \) (direction et sens uniquement) à la date t= 100 ms. Aucun calcul n'est demandé.
1.3. Représenter sur le graphe précédent, sans souci d'échelle, les forces qui s'exercent sur le volant en un des points de la portion AB. Les intensités de ces forces sont-elles du même ordre de grandeur ? Justifier en utilisant la 2ème loi de Newton.
2. Étude énergétique du mouvement
Grâce aux mesures réalisées, on a pu tracer l'évolution au cours du temps des énergies cinétique, potentielle de pesanteur et mécanique.
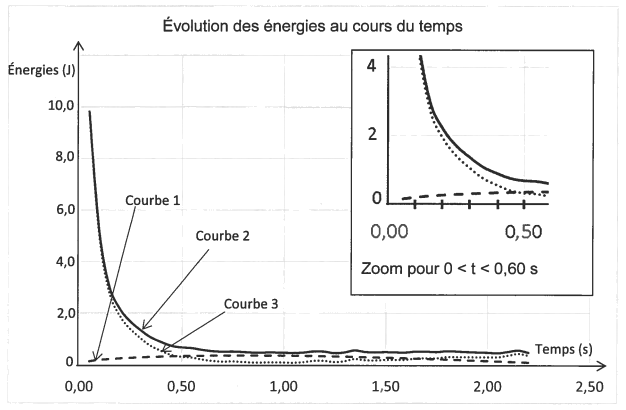
Donnée : Intensité de la pesanteur g = 9,8 m·s-2
2.1 . Identifier, en justifiant, la nature de l'énergie correspondant à chaque courbe.
2.2. À partir d'une des trois courbes précédentes, calculer en km·h-1 l'ordre de grandeur de la vitesse du volant lorsqu'il occupe la position B.
2.3. Calculer le travail du poids du volant lors du déplacement de A à B. Commenter le signe du résultat obtenu.
2.4. L'énergie mécanique, quant à elle, varie au cours du mouvement. Quelle est la cause de cette variation?
3. L'expérience de Thomas Pesquet

L'astronaute français, qui s'est envolé vers la station spatiale internationale (ISS) jeudi 17 novembre, a suscité la curiosité des internautes en diffusant une photo de sa valise contenant... un volant de badminton.
"ll s'agira de déterminer comment l'objet se comportera en apesanteur, dans la station spatiale internationale," explique le représentant du CNES.
L'Express
À bord de la station ISS, dont l'altitude de l'orbite vaut 400 km, les modules sont pressurisés pour permettre aux astronautes de respirer sans assistance. La pression de l'air y est égale à la pression atmosphérique sur Terre.
Thomas Pesquet a réalisé une expérience en apesanteur en se filmant: il lâche le volant sans vitesse initiale. Deux images extraites de la vidéo, une fois le volant lâché, sont données ci-dessous :

Données :
- Constante de gravitation universelle : G = 6,67·10-11 SI
- Rayon de la Terre : RT = 6380 km
- Masse de la Terre : MT = 5,97·1024 kg
La Terre est supposée à répartition de masse sphérique. L’ISS est considérée ponctuelle et en mouvement circulaire uniforme autour de la Terre dans le référentiel géocentrique (supposé galiléen).
3.1. Décrire le mouvement du volant lorsqu'il est lâché par Thomas Pesquet, d'abord dans le référentiel lié à l'ISS, puis dans le référentiel géocentrique.
3.2. Établir l'expression de la valeur de l'accélération de l'lSS dans le référentiel géocentrique, puis la calculer.
3.3. Expliquer pourquoi le volant reste près de l'astronaute.
|