Carnet de bac

Le problème posé par la nature des « rayons cathodiques » à la fin du XIXème siècle fut résolu en 1897 par l'Anglais J.J. Thomson : il s'agissait de particules chargées négativement baptisées par la suite « électrons ». La découverte de l'électron valut à Thomson le prix Nobel de physique en 1906.
Le défi pour les scientifiques de l'époque fut alors de déterminer les caractéristiques de cette particule : sa charge électrique et sa masse. Dans un premier temps, Thomson lui-même, en étudiant la déviation d'un faisceau d'électrons dans un champ électrique, put obtenir le « rapport e/me » de ces deux caractéristiques.
C'est cependant l'Américain R. Millikan qui, réalisant de multiples expériences entre 1906 et 1913 sur des gouttelettes d'huile, détermina la valeur de la charge de l'électron.
En 1927, G.P. Thomson, le fils de J.J. Thomson, réalise une expérience de diffraction des électrons par des cristaux.
Actuellement, les valeurs admises de la masse et de la charge de l'électron sont :
m_e = 9,1093826×10⁻³¹ kg et e = 1,602176565·10⁻¹⁹ C.

Donnée : Constante de Planck : h = 6,63·10⁻³⁴ J·s

Cet exercice comprend trois parties indépendantes, en lien avec les travaux de ces trois physiciens.

1. L'expérience de J.J. Thomson

Lors de ses recherches dans son laboratoire de Cambridge, Thomson conçoit un dispositif dans lequel un faisceau d'électrons est dévié lors de son passage entre deux plaques où règne un champ électrique. La mesure de la déviation du faisceau d'électrons lui permet alors de déterminer le rapport e/m_e.

L'étude suivante porte sur le mouvement d'un électron du faisceau qui pénètre entre deux plaques parallèles et horizontales P₁ et P₂, dans une zone où règne un champ électrique \(\displaystyle \mathrm{ \vec{E} }\) supposé uniforme et perpendiculaire aux deux plaques.

À l'instant t = 0 s, l'électron arrive en un point O avec une vitesse horizontale \(\displaystyle \mathrm{ \vec{v}_0 }\) . La trajectoire de l'électron dans un repère (O,x,y) est fournie sur L'annexe à rendre avec la copie. L'électron de masse me et de charge q = − e, dont le mouvement étudié dans le référentiel terrestre supposé galiléen, est soumis à la seule force électrostatique \(\displaystyle \mathrm{ \vec{F}_e }\) .

1.1. Sur le document de L'annexe à rendre avec la copie, représenter sans souci d'échelle et en justifiant les tracés :
- le vecteur force \(\displaystyle \mathrm{ \vec{F}_e }\) en un point de la trajectoire de l'électron ;
- le vecteur champ électrique \(\displaystyle \mathrm{ \vec{E} }\) en un point quelconque situé entre les plaques P₁ et P₂.

1.2. En utilisant la deuxième loi de Newton, déterminer les équations horaires x(t) et y(t) du mouvement de l'électron.

1.3. Vérifier que la trajectoire de l'électron a pour équation : \(\displaystyle \mathrm{ y = \frac{e \ E}{2 \ m_e \ v_0^2} x^2 }\) .

1.4. À la sortie de la zone entre les plaques P₁ et P₂, l'électron a subi une déviation verticale SH comme l'indique le schéma de L'annexe à rendre avecla copie. On mesure SH = y_S = 2,0·10⁻² m. Déterminer, dans cette expérience, la valeur du rapport e/me de l'électron. Conclure.

Données :

• Longueur des plaques : L = 9,0·10⁻² m
• Vitesse initiale de l'électron : v₀ = 2,4·10⁷ m·s⁻¹
• Valeur du champ électrique : E = 1,6·10⁴ V·m⁻¹

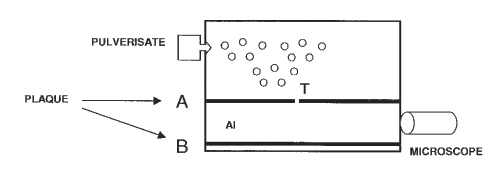
Millikan pulvérise des gouttelettes d'huile chargées par irradiation entre deux plaques planes où règne un champ électrique et les observe à l'aide d'un microscope. Sa méthode consiste à immobiliser les gouttelettes en augmentant le champ électrique jusqu'à ce que le poids de la gouttelette soit compensé par la force électrostatique. Millikan parvint ainsi à obtenir une valeur approchée de la charge élémentaire e = 1,591·10⁻¹⁹ C, très proche de la valeur admise aujourd'hui.

Un pulvérisateur produit un nuage de gouttelettes d'huile chargées négativement qui tombent dans la chambre supérieure du dispositif. Lorsque l'une d'elles passe à travers le trou T, elle tombe verticalement à une vitesse constante v₁, son poids étant très vite compensé par la force de frottement exercée par l'air. Lors de cette première étape, la chute verticale de la gouttelette dans l'air en l'absence de champ électrique est observée à l'aide d'un microscope et permet de déterminer le rayon r de la gouttelette qui n'est pas mesurable directement. Lors d'une deuxième étape, lorsque la gouttelette parvient en bas du dispositif, un champ électrique uniforme est créé entre les plaques A et B. La gouttelette remonte alors verticalement à une vitesse constante v₂. La charge électrique portée par la gouttelette est ensuite déduite des mesures des vitesses v₁ et v₂.

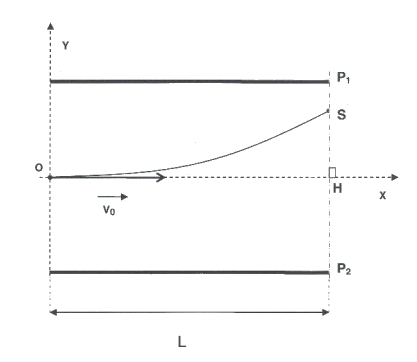
Lors de l'expérience menée au laboratoire, une gouttelette de masse m et de charge q négative arrive entre les plaques A et B. La poussée d'Archimède est négligée. La gouttelette étudiée est soumise à son poids \(\displaystyle \mathrm{ \vec{P} }\) et à la force de frottement \(\displaystyle \mathrm{ \vec{f} }\) exercée par l'air s'exprimant par la relation \(\displaystyle \mathrm{ \vec{f}= -6 \ π \ η \ r \ \vec{v} }\) dans laquelle η est la viscosité de l'air, r le rayon de la gouttelette et sa vitesse \(\displaystyle \mathrm{ \vec{v} }\).
Données :

• Masse volumique de l'huile : ρ = 890 kg·m⁻³
• Valeur du champ de pesanteur : g = 9,8 N·kg⁻¹
• Viscosité de l'air : η = 1,8·10−5 kg·m⁻¹·s⁻¹

2.1. Chute verticale de la gouttelette

2.1.1. Lors de la chute de la gouttelette en l'absence de champ électrique, écrire la relation vectorielle entre la force de frottement et le poids lorsque la vitesse constante v₁ est atteinte. En déduire l'expression de v₁ en fonction de η, r, m et g.

2.1.2. La relation précédente peut également s'écrire \(\displaystyle \mathrm{ v_1= \frac{2 \ ρ \ g \ r^2}{9 \ η} }\) où ρ est la masse volumique de l'huile. Déterminer le rayon r de la gouttelette sachant qu'elle parcourt, lors de sa chute, une distance de 2,11 mm pendant une durée Δt =10,0 s.

2.1.3. Afin de faciliter la mesure au microscope, la gouttelette ne doit pas être trop rapide. En déduire s'il est préférable de sélectionner une grosse gouttelette ou au contraire une petite gouttelette.

2.2. Remontée de la gouttelette

Un champ électrique uniforme étant établi entre les plaques A et B, la gouttelette subit une force supplémentaire \(\displaystyle \mathrm{ \vec{F}_e }\) verticale et remonte alors avec une vitesse constante v₂ atteinte presque instantanément. On peut montrer que la charge q de la gouttelette est donnée par la relation : \(\displaystyle \mathrm{ q=- \frac{6 \ π \ η \ r \ (v_1+v_2)}{E} }\) Plusieurs mesures ont été réalisées pour différentes gouttelettes et rassemblées dans le tableau du document 3.

2.2.1. Les gouttelettes n°2 et n°5 du document 3 ont la même vitesse de descente v₁ mais des vitesses de remontée v₂ différentes. Déterminer sans calcul le rayon de la gouttelette n°5. Justifier. Pourquoi leurs vitesses de remontée sont-elles différentes ?

2.2.2. Montrer, à partir des résultats expérimentaux du document 3, que la charge de ces gouttelettes est « quantifiée », c'est-à-dire qu'elle ne prend que des valeurs multiples d'une même charge élémentaire égale à 1,6·10⁻¹⁹ C.

2.3. En quoi le protocole de l'expérience effectuée par Millikan diffère-t-il de celui réalisé au laboratoire par J.J. Thomson ?