Carnet de bac

La mesure du temps est une question essentielle depuis... la nuit des temps. Elle a initialement été basée sur l’observation d’un phénomène régulier et répétitif qui permettait de caractériser des durées égales.

1. La mesure du temps par Galilée

Galilée, au XVIIème siècle, a eu l’idée d’utiliser un pendule pour mesurer le temps :

« J’ai pris deux boules, l’une de plomb et l’autre de liège, celle-là au moins cent fois plus lourde que celle-ci, puis j’ai attaché chacune d’elles à deux fils très fins, longs tous les deux de quatre coudées ; les écartant alors de la position perpendiculaire, je les lâchais en même temps ; une bonne centaine d’allées et venues, accomplies par les boules elles-mêmes, m’ont clairement montré qu’entre la période du corps pesant et celle du corps léger, la coïncidence est telle que sur mille vibrations comme sur cent, le premier n’acquiert sur le second aucune avance, fût-ce la plus minime, mais que tous les deux ont un rythme de mouvement rigoureusement identique. On observe également l’action du milieu qui, en gênant le mouvement, ralentit bien davantage les vibrations du liège que celles du plomb, sans toutefois modifier leur fréquence.

D’après Discours et démonstrations mathématiques concernant deux sciences nouvelles, publié en 1636

• Une coudée = 0,573 m
• Accélération de la pesanteur : g = 9,81 m·s^-2
• La masse du pendule de plomb de Galilée est : m = 50 g

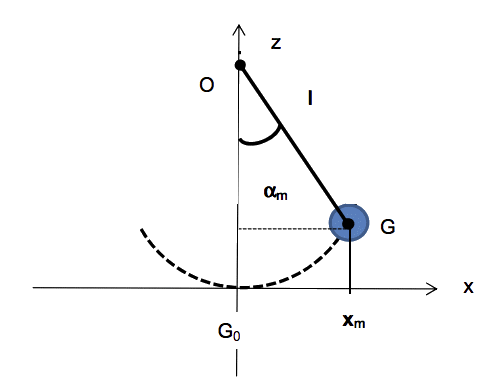
On réalise un pendule en suspendant une bille de plomb de masse m = 50 g et de centre d’inertie G, à un fil de longueur l accroché en O comme l’indique la figure du document 2.

On choisit la position à l’équilibre G₀ de G comme origine des altitudes z. Pour un amortissement faible, la pseudo-période T du pendule est voisine de sa période propre T₀. L’expression de la période propre du pendule est l’une des propositions suivantes :
\(\displaystyle\mathrm{ T_0 = 2 \ π \ \sqrt{ℓ} } \) ; \(\displaystyle\mathrm{ T_0 = 2 \ π \ \sqrt{\frac{ℓ}{g}} } \) ; \(\displaystyle\mathrm{ T_0 = 2 \ π \ \sqrt{\frac{g}{ℓ}} } \) ; \(\displaystyle\mathrm{ T_0 = 2 \ π \ \sqrt{\frac{m}{ℓ}} } \)
ℓ désigne la longueur du fil et m la masse du pendule. Un système informatique permet d’obtenir les mesures représentées sur les deux graphes du document 3 de l’annexe.

1.1. À l’aide des documents et de vos connaissances, proposer une réponse argumentée pour montrer que « le pendule réalisé aurait pu être celui de Galilée ! ».

Pour cela : À l’aide d’une analyse dimensionnelle, choisir l’expression de la période du pendule simple qui convient parmi celles proposées. Comparer de la manière la plus précise possible, la valeur calculée de la période du pendule de Galilée à celle du pendule réalisé expérimentalement, puis conclure.

1.2.
1.2.1. Déterminer à partir du document 3 (fenêtre 1) la valeur de l’abscisse x_m. En déduire la valeur de l’angle maximal α_m, en degré, décrit par le pendule.

1.2.2. Calculer la vitesse maximale vm atteinte par le centre d’inertie G.

1.2.3. Tracer sur le document 3 (fenêtre 2) de l’annexe en page 14 à rendre avec la copie les évolutions de l’énergie mécanique et de l’énergie potentielle de pesanteur, en fonction de l’abscisse x du centre d’inertie G du pendule réalisé.

2. La molécule d’ammoniac

Avec l’horloge atomique – conçue à partir des années 1950/60 – la mesure du temps bascule dans le temps de l’infiniment petit. Ce ne sont plus les oscillations régulières d’un pendule ou d’un ressort spiral qui donnent le rythme à l’horloge. Ici, ce sont les vibrations extrêmement rapides d’une molécule ou d’atome que l’homme a su mettre au profit de la mesure du temps.

Dans les années 1960, il a été décidé de détacher la mesure du temps de l’astronomie et de redéfinir le temps en fonction des vibrations d’une molécule ou d’un atome. Une des premières horloges de ce type mettait en jeu les oscillations de la molécule d’ammoniac. (…) Les molécules d’ammoniac ont la forme d’un parapluie, elles peuvent ainsi se retourner de la même façon que cet objet par grand vent (voir schéma cidessous) ! En effet, en faisant un aller-retour d’une forme « normale » à une forme « retournée » à un rythme régulier de 24 milliards de fois par seconde (!), ces molécules permettent de concevoir un dispositif horloger d’une stabilité inégalée…

D’après L'horloge atomique

2.1. Quelle est la période de retournement de la molécule d’ammoniac ?

2.2. La molécule d’ammoniac est constituée d’un atome d’azote et de trois atomes d’hydrogène. Écrire la formule de Lewis de la molécule d’ammoniac et proposer une représentation de Cram spatiale de la molécule. Données : N (Z = 7) ; H (Z = 1)

2.3. L’ammoniac est une base, mise en jeu dans l’équilibre suivant :

NH_{3 (aq)}+ H₃O⁺_(aq) ⇆ NH₄⁺_(aq) + H₂O_(ℓ)

Recopier l’équation ci-dessus et expliquer la formation de l’ion ammonium NH₄⁺.

2.4. Donnée : La constante d’acidité de l’ion ammonium NH₄⁺ à 25°C est K_A= 5,6·10^-10.

Parmi les 4 propositions suivantes une seule affirmation est vraie. Justifier que les 3 autres sont fausses.
➀ Le pK_A de l’ion ammonium est 10,2.
➁ La réaction de dissociation de l’ion ammonium dans l’eau s’écrit :
➂ L’ion ammonium est totalement dissocié dans l’eau.
➃ Dans une solution aqueuse d’ammoniac de pH égal à 8, l’espèce prédominante est NH₃.

Document 3