Carnet de bac

La découverte du laser il y a cinquante ans a révolutionné les domaines industriels, médical, technologique… Si le principe fondamental du laser a été décrit dès 1917 par Albert Einstein, le premier laser a été fabriqué en 1960 par Théodore Maiman. Depuis les lasers sont très présents dans notre quotidien.
L’objectif de cet exercice est d’étudier l’apport de la diode laser dans le stockage optique.

« Les diodes laser sont des lasers qui utilisent comme milieu amplificateur un solide obtenu à partir de matériaux semi-conducteurs, matériaux qui n’existent pas à l’état naturel. Elles permettent d’obtenir pour un coût réduit des lasers très efficaces : ces lasers semi-conducteurs ont aujourd’hui pris une très grande importance et représentent une grande partie du marché total des lasers. On les utilise pour transporter l’information échangée par téléphone ou internet, ils lisent les DVD ou les codes-barres dans les supermarchés. Comment ces lasers ont-ils pris tant d’importance ? La possibilité d’en fabriquer des milliers en même temps a conduit à un faible coût de fabrication. À cela s’ajoute leur excellent rendement et leur compacité : ces lasers s’étendent sur quelques dixièmes de millimètres et leur épaisseur est de l’ordre du micron, soit environ vingt fois moins que l’épaisseur d’une feuille d’aluminium. »

D’après Introduction : Le laser de F. Bretenaker, N. Treps

« L’émission de lumière a lieu dans une zone de jonctions de semi-conducteurs, lorsqu’on applique une tension électrique. En régime d’émission spontanée, on a une diode électroluminescente (DEL), composant de base de nombreux afficheurs. Mais si le courant électrique injecté dans la jonction augmente, on peut atteindre le régime où l’émission stimulée est prédominante : on obtient une diode laser. »

D’après Introduction aux lasers et à l’optique quantique de G.Grynberg, A.Aspect, C.Fabre

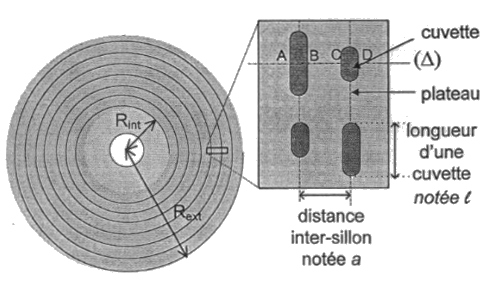
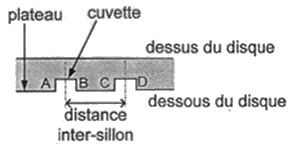
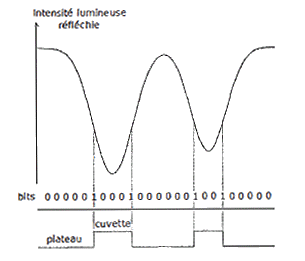
Sur un disque optique (CD, DVD, disque blu-ray), les données sont inscrites sur une surface ayant la forme d’une couronne de rayon intérieur R_int=2,5 cm et de rayon extérieur R_ext=5,8 cm. Les données sont gravées sous forme de minuscules cuvettes, placées sur des sillons le long de la piste. Les espaces entre les cuvettes sont appelées plateaux (voir figures 1.a et 1.b)

Figure 1.a - Vue de dessous des sillons d'un disque optique

Figure 1.b - Vue en coupe suivant l'axe (Δ) de deux sillons d'un disque

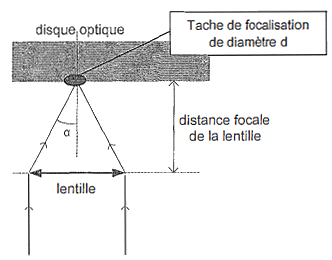
Afin de lire les données du disque, un faisceau lumineux issu d’une diode laser est focalisé par une lentille sur le disque optique. Un chariot délace le dispositif de façon à permettre au faisceau laser de balayer l’intégralité du disque optique (voir figure 2).

Une fois focalisé, le spot laser apparaît sur le disque sous forme d’une tache de diamètre : \(\displaystyle\mathrm{ d=\frac{1,22 \ λ}{sin \ α} }\) où λ est la longueur d’onde du faisceau laser et sin α la valeur de l’Ouverture Numérique (O.N. = sinα) de la lentille utilisée. Figure 3 - Allure de l'intensité lue et codage binaire associé pour un profil de piste

Figure 2 - Dispositif de focalisation du faisceau laser sur le disque optique Le faisceau se réfléchit sur le disque optique puis est renvoyé vers le capteur de lumière (photodiode) qui détecte l’intensité lumineuse. L’intensité est ensuite codée sous forme binaire, le code binaire étant directement lié au profil de la piste lue (figure 3).

• Célérité de la lumière dans le vide c = 3,00·10⁸ m·s^-1 ;
• Constante de Planck : h = 6,63·10^–34 J·s ;
• Domaine fréquentiel du son audible pour l’oreille humaine : entre 20 Hz et 20 kHz ;
• Caractéristiques des différents types de supports (CD, disque blu-ray) ;

  	CD ou CD-ROM	Blu-ray
  Longueur d’onde λ du faisceau laser	780 nm	405 nm
  Ouverture numérique de la lentille O.N.	0,45	0,85
  Distance inter-sillon sur le disque a	1,67 µm	0,32 µm
  Longueur minimale d’une cuvette ℓ	0,83 µm	0,15 µm

• Spectre de la lumière visible :

  λ (nm)	400-445	445-475	475-510	510-570	570-590	590-600	600-800
  couleur	violet	indigo	bleu	vert	jaune	orange	rouge

• 1 octet = 8 bits ;
• Théorème de Shannon relatif à l’échantillonnage : La fréquence d’échantillonnage d’un signal doit être égale ou supérieure au double de la fréquence maximale contenue dans ce signal, afin de le numériser correctement ;
• Pas en tension électrique p d’un convertisseur analogique-numérique : il correspond au plus petit écart de tension entre deux points du signal numérisé. Il est relié au nombre de bits n et à la tension maximale U_max du convertisseur par la relation : \(\displaystyle\mathrm{ p = \frac{U_{max}}{2^n-1} }\) .

Les trois parties sont indépendantes les unes des autres.

1. Lecture d’un disque optique

1.1. Les diodes lasers utilisées dans les lecteurs blu-ray émettent une lumière de longueur d’onde λ = 405 nm. Calculer l’énergie d’un photon associé à cette radiation.

1.2. Indiquer le processus d’émission d’une DEL et d’un laser et indiquer au moins deux caractéristiques de la lumière émise par le laser.

1.3. On admet que la profondeur d’une cuvette est égale à λ/4, où λ est la longueur d’onde du faisceau laser utilisé. Pour chacun des cas (a) et (b) du document 3, calculer la distance supplémentaire δ parcourue par le rayon (2) par rapport au rayon (1).

1.4 Le dispositif optique précédent permet aux rayons (1) et (2) d’interférer après réflexion sur le disque optique.

1.4.1. Comparer l’intensité lumineuse du faisceau réfléchi sur un plateau avec celle du faisceau réfléchi dans une cuvette.

1.4.2. Préciser dans chacun des deux cas précédents la nature des interférences (constructives ou destructives).

1.5. Comment les variations d’intensité lumineuse sont-elles associées aux « bits » (de valeur 0 ou 1) ?

2. Traitement de l’information numérique

Sur la documentation technique d’un CD-ROM audio, on lit les informations suivantes :

Le son est enregistré sous forme d’échantillons à 44,1 kHz avec 16 bits par canal. Sachant qu’il y a deux canaux de son stéréophonique, le débit binaire est donc de 176 ko·s^-1 (kilooctets par seconde). Le CD-ROM de capacité 780 Mo, peut contenir 74 minutes de son.

2.1. Justifier la valeur de la fréquence d’échantillonnage utilisée pour numériser le son.

2.2. On suppose que le convertisseur analogique-numérique utilisé pour l’échantillonnage fonctionne avec une tension maximale U_max = 10 V. Calculer le pas en tension de ce convertisseur.

2.3. À partir de la valeur de la fréquence d’échantillonnage, retrouver par le calcul la valeur du débit binaire mentionné dans la notice technique.

2.4. Retrouver la capacité de stockage exprimée en Mo (mégaoctets) d’un CD-ROM audio pouvant contenir 74 minutes de son.

2.5. Si on enregistrait un signal purement audio de même débit sur un disque blu-ray affichant une capacité de 22 Go, quelle serait la durée de lecture en heures ?

3. Capacité de stockage d’un disque optique

3.1. Proposer une justification à l’appellation « blu-ray ».

3.2. Calculer la capacité de stockage (nombre de bits stockés) d’un CD-ROM. Cette capacité devra être exprimée en Mo (mégaoctets). En première approximation, on considère qu’un bit de donnée occupe sur le disque optique une surface effective estimée à s = ℓ a.
Surface d’une couronne : S_C = ( R_ext² - R_int²) π

3.3. À partir de vos connaissances et des documents fournis, rédigez un paragraphe argumenté répondant à la question suivante (10 lignes environ) : Quels paramètres physiques du lecteur et du disque blu-ray permettent d’obtenir une capacité de stockage du disque blu-ray bien supérieure à celle du CD-ROM ?