Carnet de bac
Annales
La mesure du temps |
|
| Antilles 2013 - Exercice 1 - 5 points |
|
Pour mesurer le temps, plusieurs méthodes ou instruments ont été élaborés. Les différents documents ci-dessous présentent quelques-unes de ces méthodes. |
||||
|
Document 1
Les hommes préhistoriques étaient conscients de la notion de jours et de nuits ainsi que de la succession des saisons. La mesure du temps est le plus ancien problème technique que les hommes ont eu à résoudre. Le Soleil et la Lune, les deux astres les plus visibles, furent les premières horloges
utilisées par les hommes.
|
||||
|
Document 2 : Mesurer le temps à l’aide d’un cadran solaire (≈ 600 avant Jésus-Christ en Grèce)
Le cadran solaire est une surface plane dans laquelle est plantée une tige appelée style. La direction de l’ombre indique l’heure au soleil. Le cadran est divisé en douze heures du lever au coucher du soleil, mais comme la durée du jour varie selon les saisons, la durée des heures varie également... Plus tard, le perfectionnement de la graduation du cadran et l’orientation du style permettront d’augmenter la fiabilité de l’instrument.
Les instruments de mesure du temps, Musée de l’horlogerie de Saint Nicolas d’Aliermont |
||||
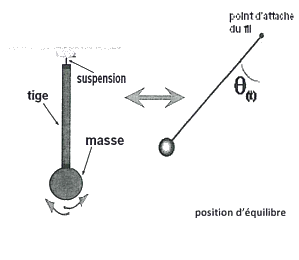
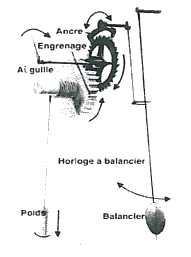
Document 3 : Mesurer le temps à l’aide d’oscillateurs mécaniques (XIIIème au XXème siècle, Europe)
|
||||
|
Document 4 : Mesurer le temps à l’aide d’une horloge à quartz (1930)
Une horloge à quartz est un dispositif qui met en jeu une propriété de certains matériaux appelée la piézoélectricité. Excité par un courant électrique, un cristal de quartz peut osciller. On réalise alors un oscillateur électrique vibrant à une fréquence très précise de 32 768 Hz. Un circuit diviseur de fréquence permet d’obtenir une impulsion par seconde. Les impulsions sont ensuite transmises soit à un système mécanique permettant de faire tourner les aiguilles, soit à un système électronique permettant d’afficher l’heure. Une horloge à quartz dérive seulement d’une seconde tous les six ans. |
||||
|
Document 5 : Mesurer le temps à l’aide d’une horloge atomique (1950)
Les horloges atomiques ont été mises au point dès le milieu des années 1950. Leur précision et leur stabilité sont telles qu’elles constituent aujourd’hui les étalons de temps (ou de fréquence). Depuis la Conférence générale des poids et mesures de 1967, « la seconde est la durée de 9 192 631 770 périodes de la radiation correspondant à la transition entre les deux niveaux énergétiques dits hyperfins de l’état fondamental de l’atome de césium 133 ».
Source : Les horloges atomiques |
||||
|
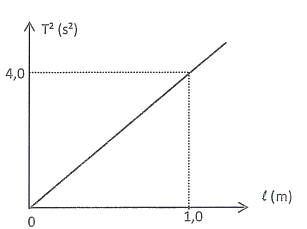
1. À l’aide du document 3.b. expliquer, en justifiant, quelle est la formule donnant la variation de la période T d’un pendule en fonction de la longueur ℓ de la tige (C est une constante réelle).
| ||||